Машинное обучение (ML) находится на стыке компьютерных наук и математики. ML использует сложные математические концепции для создания алгоритмов, способных обучаться на данных и делать прогнозы. Насколько высокий уровень математических знаний нужно иметь, чтобы без труда разобраться в передовых методах машинного обучения? Посмотрите любую серьезную ML-статью на arxiv.org, например эту: если формулы в ней не кажутся вам иероглифами, то с вашим уровнем математики все в порядке.
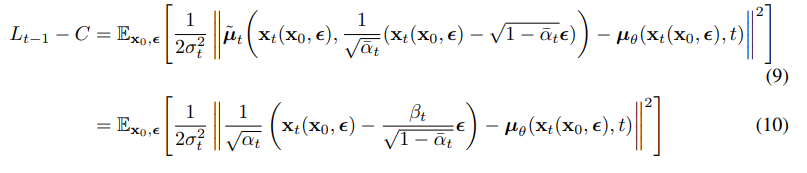
Изучение фундаментальной математики похоже на то, как мы учимся читать. Как только мы научимся читать, перед нами открывается целый мир новых знаний. Без этого навыка доступ к этим знаниям закрыт. Точно так же, без понимания основ математики невозможно двигаться дальше в машинном обучении – все дальнейшие темы будут просто недоступны.
Математика для ML: что действительно нужно знать
Дорожная карта для перехода от школьной математики к передовому ML включает 4 основных этапа.
1. Базовая математика
Базовая математика. Фундаментальная математика необходима для понимания того, как работают модели машинного обучения и как они обучаются на данных. Для большинства людей этот этап – самый сложный, переломный момент на пути к машинному обучению. Именно на этой ступени многие бросают обучение. В необходимую математическую базу входят:
1.1. Алгебра
Алгебра – фундаментальный раздел математики, который формирует основу для большинства математических операций и вычислений в машинном обучении. Ключевые концепции:
- Уравнения и неравенства – важно уметь решать линейные и нелинейные уравнения, так как они часто возникают при обучении моделей, например, в задачах оптимизации.
- Полиномы – многие функции, которые используются в машинном обучении, могут быть приближены полиномами.
- Логарифмы и экспоненты – широко используются в функциях активации нейронных сетей, расчетах вероятностей и задачах оптимизации.
1.2. Математический анализ
Математический анализ – дифференциальное и интегральное исчисление функций одной переменной. Помогает понимать поведение функций и их изменения. В машинном обучении эти понятия часто встречаются в задачах, связанных с настройкой гиперпараметров модели и минимизацией ошибок:
- Пределы и непрерывность – важны для понимания функций потерь и того, как они зависят от параметров модели.
- Производные – широко используются в задачах оптимизации, где необходимо минимизировать функции потерь с помощью методов градиентного спуска.
- Интегралы – применяются для нахождения площадей под кривыми и в вероятностных расчетах, например, при вычислении функций распределения.
1.3. Линейная алгебра
Линейная алгебра – важнейший инструмент для работы с многомерными данными и построения сложных моделей. Лежит в основе многих алгоритмов машинного обучения, особенно тех, что работают с большими объемами данных. Основные темы:
- Векторы и матрицы – применяются для представления данных (например, векторы признаков).
- Операции над матрицами – знание операций сложения, умножения, транспонирования матриц необходимо для работы с алгоритмами машинного обучения.
- Определители и обратные матрицы – используются в некоторых алгоритмах, таких как метод наименьших квадратов.
- Собственные значения и собственные векторы – применяются в методах снижения размерности данных (например, PCA – метод главных компонент).
1.4. Теория вероятностей и статистика
Играют ключевую роль в понимании того, как работают модели машинного обучения и как интерпретировать их результаты. Основные моменты:
- Основы теории вероятностей – вероятность событий, условные вероятности, байесовская статистика – все это критично для создания вероятностных моделей.
- Распределения вероятностей – нормальное распределение, распределение Пуассона и другие – часто используются для моделирования случайных процессов.
- Оценка параметров и гипотез – необходимо понимать, как оценивать параметры моделей и проверять гипотезы, например, используя тестирование гипотез и доверительные интервалы.
- Корреляция и ковариация – помогают выявить связи между переменными, что важно при выборе признаков для модели.
1.5. Основы многомерного анализа
Основы многомерного анализа – интегральное и дифференциальное исчисление для функций с несколькими переменными. Знание многомерного анализа важно для работы со сложными моделями машинного обучения, где требуется оптимизация в многомерных пространствах. Необходимые темы:
- Частные производные – используются в многомерных задачах оптимизации для расчета градиентов в методе градиентного спуска.
- Градиенты и гессианы – важны для определения направления и скорости изменения функций потерь в многомерном пространстве параметров.
- Многомерные интегралы – применяются для расчета вероятностей в многомерных пространствах и в методах Монте-Карло.
2. Классическое машинное обучение
На этом этапе нужно научиться писать код для базовых моделей регрессии и классификации, чтобы самостоятельно реализовать, например, модель линейной регрессии (для предсказания числового значения) и логистической регрессии (для классификации данных на категории). Также надо разобраться в архитектуре небольших многослойных нейросетей.
3. Глубокое обучение
Надо научиться создавать многослойные нейронные сети с большим числом параметров. Архитектура сети будет подбираться под конкретные задачи: компьютерное зрение, обработка текста и так далее. Здесь уже нужно понимать, как оптимизировать сеть, выбирать правильные гиперпараметры и использовать мощные инструменты для работы с большими объемами данных.
4. Передовые технологии машинного обучения
Здесь изучаются самые современные и продвинутые модели: трансформеры, большие языковые модели (LLM), диффузионные модели и другие новейшие методы. Именно они вызывают у начинающих интерес к машинному обучению и привлекают внимание исследователей и разработчиков по всему миру.
Почему не стоить изучать математику для ML по обычным учебникам
В интернете достаточно бесплатных материалов, и при желании математику можно изучать самостоятельно. Следует, однако, отдавать предпочтение книгам и курсам, которые изначально создавались с учетом ML-специфики. Обычные учебники не подходят потому, что далеко не каждый раздел математики используется в ML полностью. Например, из раздела дифференциального исчисления для функций с несколькими переменными обязательно нужно знать, как вычислять градиенты. Градиенты постоянно используются в методах оптимизации, таких как градиентный спуск, который помогает обучать модели машинного обучения. Также важно хорошо понимать цепное правило дифференцирования сложных функций. Эти концепции лежат в основе алгоритма обратного распространения ошибки, который используется для обучения нейронных сетей.
В то же время дивергенция, ротор, сферические координаты и теорема Стокса вообще не встречаются в машинном обучении. Эти понятия важны в физике и многих других областях, но для работы с ML их знать не нужно. Вреда от лишних знаний, конечно же, не будет, но у такого широкоохватного подхода есть два серьезных минуса:
- Много времени будет потрачено на изучение аспектов, которые никогда не пригодятся в работе.
- Чем обширнее и сложнее программа подготовки, тем выше вероятность сдаться раньше времени и не дойти до цели вообще.
А специализированные книги и курсы, напротив, предлагают несколько весомых преимуществ (помимо сжатой программы):
- Практические примеры – работа с градиентным спуском, матрицами признаков или вероятностными моделями, которые помогают лучше понять, как математические концепции применяются в машинном обучении.
- Развитие интуитивного понимания специфических математических подходов, например, регуляризации для предотвращения переобучения или использования градиентных методов для минимизации функций потерь.
- Современные методы и алгоритмы. Машинное обучение – быстро развивающаяся область, и специализированные книги часто содержат новейшие подходы и методы, которые еще не вошли в общие учебники математики.
Как не потерять мотивацию
Человеку с математическим образованием эта дорожная карта вряд ли покажется сложной, но для большинства остальных людей объем математики, необходимый для ML, выглядит пугающим. Чтобы не потерять мотивацию, стоит иногда отвлекаться – на чтение статей о передовых исследованиях, тестирование новых моделей машинного обучения и эксперименты с библиотеками. Это поможет поддержать живой интерес и энтузиазм. Также важно помнить, что после того, как вы освоите фундаментальную математическую базу и классическое машинное обучение, дело пойдет гораздо проще: вам уже будет по силам процесс создания и дообучения моделей по описаниям в публикациях на arxiv.org, а это откроет вход в ML-нишу на джуниорскую позицию.
Математика для Data Science: от основ к ML
Хочешь стать экспертом в Machine Learning и Data Science? Начни с фундамента. Наш курс математики для Data Science раскрывает ключевые концепции, необходимые для успеха в мире AI и ML.
🔢 Что ты получишь:
- Глубокое понимание математических концепций, применяемых в ML
- Навыки работы с реальными данными и моделями
- Уверенность в интерпретации сложных алгоритмов
📊 Программа курса:
- Школьная математика
- Математический анализ
- Линейная алгебра
- Комбинаторика
- Теория вероятностей и математическая статистика
- Машинное обучение
💡 Особенности обучения:
- Интерактивные задания на реальных датасетах
- Разбор кейсов из индустрии
- Поддержка опытных менторов
Независимо от твоего текущего уровня, этот курс поможет тебе построить прочный фундамент для карьеры в Data Science и машинном обучении.




Комментарии