Алгоритм Укконена предназначен для построения суффиксного дерева из строки. На момент создания (в 1995 году) он был самым эффективным алгоритмом в своем роде:
- При наивном подходе суффиксное дерево можно создать лишь за O(n3), в лучшем случае за O(n2), а решение Укконена выполняется за линейное время.
- Существующие алгоритмы построения суффиксных деревьев, предложенные Вайнером (в 1973 году) и МакКрейтом (в 1976 году), относятся к оффлайновым, то есть для начала работы им нужна вся строка целиком, а алгоритм Укконена – онлайновый и работает последовательно.
Алгоритм не свободен от недостатков – суффиксное дерево должно быть полностью загружено в оперативную память, что может привести к проблемам при очень больших входных данных или алфавитах. Для обработки небольшого объема текстовых данных проще использовать префикс-функцию, а для работы с очень большими объемами данных лучше подходят кэш-эффективные алгоритмы, оптимизированные для выполнения на современных процессорах.
Тем не менее, для решения определенного класса задач со средним объемом данных алгоритм Укконена подходит отлично, а процесс реализации этого метода станет полезным опытом для любого разработчика.
Что такое суффиксное дерево
Суффиксное дерево – это компактное, сжатое древовидное представление всех суффиксов данной строки. Каждый путь от корня к листу соответствует одному суффиксу исходной строки. Суффиксные деревья позволяют очень быстро находить вхождения подстрок в строку, и благодаря этому:
- Существенно упрощают решение некоторых важных задач, связанных с обработкой текста (поиск паттернов и сжатие).
- Находят широкое применение в вычислительной биологии и биоинформатике (анализ белковых последовательностей, ДНК, поиск точных совпадений).
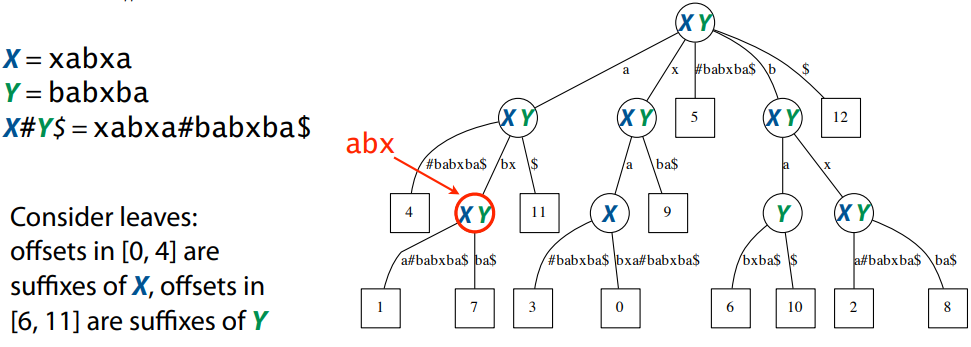
Продемонстрируем компактность суффиксных деревьев на конкретном примере.
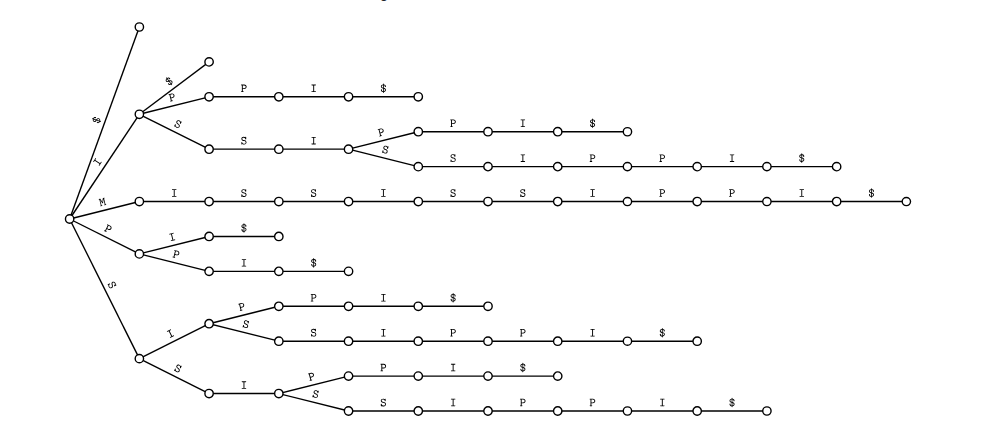
Так выглядит концептуальное древовидное представление строки MISSISSIPPI$, которая имеет 12 непустых суффиксов:
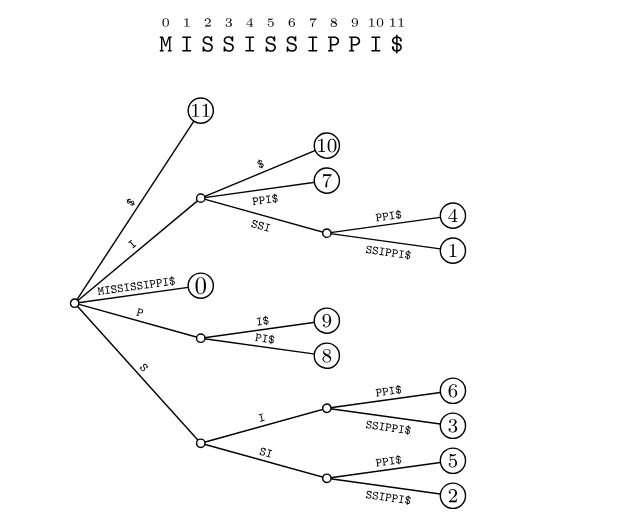
Эта же строка в виде сжатого суффиксного дерева выглядит гораздо компактнее:
Как работает алгоритм Укконена
Алгоритм Укконена строит суффиксное дерево для строки S длиной n, разбивая процесс на n отдельных фаз. На первой фазе он создает суффиксное дерево T1, содержащее только первый символ строки S.
Затем, на каждой последующей фазе i (где i идет от 2 до n):
- Алгоритм берет уже построенное суффиксное дерево Ti-1 для префикса S[1..i-1].
- Он расширяет это дерево, добавляя i-ый символ строки S к концу всех путей в дереве.
- Вместо создания новых вершин для каждого добавленного пути, алгоритм использует технику неявного суффиксного дерева.
- Он ссылается на уже существующие вершины в Ti-1 и хранит только дополнительную информацию (индексы, ссылки) для представления новых суффиксов.
- В результате получается неявное суффиксное дерево Ti для префикса S[1..i].
Таким образом, на каждом шаге алгоритм расширяет существующее дерево, избегая создания многочисленных повторяющихся вершин, благодаря использованию неявных ссылок и индексов. В финале получается полное неявное суффиксное дерево для всей строки S.

Курс «Алгоритмы и структуры данных»
Курс «Алгоритмы и структуры данных» для тех, кто хочет научиться работать с алгоритмами, подготовиться к собеседованию в технологическую компанию или участвовать в сложных проектах.
После изучения вы:
- Узнаете о популярных алгоритмах и структурах данных
- Получите практический опыт решения сложных алгоритмических задач
- Сможете легко пройти техническое собеседование
Программа обучения
- Введение. Производительность алгоритмов
- Работа с числами
- Массивы
- Списки. Стек, очередь, дек
- Очередь с приоритетом
- Основы сортировки
- Порядковые статистики
- Деревья
- Хеш-таблицы
- Жадные алгоритмы. Динамическое программирование
- Графы и рекурсия
- Строки
- Криптография
- Длинные числа. Итоги
Неявное суффиксное дерево
Основная идея неявного суффиксного дерева заключается в том, чтобы не хранить явно все вершины дерева, а использовать специальную технику ссылок для их имитации. Вместо того чтобы создавать новую вершину для каждого префикса суффикса, в НСД используются ссылки на уже существующие вершины и позиции в исходной строке. Это достигается с помощью:
- Суффиксных ссылок. Каждая вершина содержит ссылку на каноническую вершину, представляющую тот же суффикс, что и вершина, но без первого символа.
- Точек продолжения. Для каждого суффикса имеется точка входа в уже построенное суффиксное дерево, называемая точкой продолжения.
Фаза добавления символа
На каждой фазе i алгоритм выполняет i расширений, добавляя новый символ S[i] к концам всех суффиксов S[j..i-1], где j=1..i. Существует 3 правила расширения:
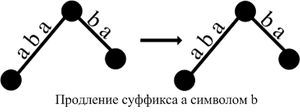
- Продление листа. Если путь от корня, помеченный S[j..i-1], заканчивается в листе, то символ S[i] просто добавляется в метку этого ребра.
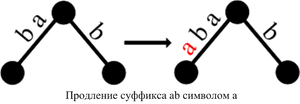
- Ответвление. Если путь заканчивается в вершине, не являющейся листом, а следующий символ отличается от S[i], то создается новый лист с меткой, начинающейся с S[i]. Может также создаваться новая внутренняя вершина, если путь заканчивается посередине ребра.
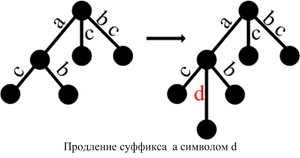
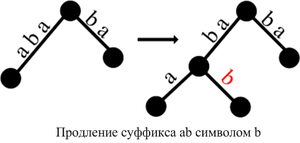
- Ничего не делать. Если путь заканчивается в вершине, из которой есть путь по si, то ничего делать не надо.
Суффиксные ссылки
Для эффективного нахождения конца текущего пути в дереве используется вспомогательная структура – суффиксные ссылки. Каждая внутренняя вершина v хранит ссылку на вершину, представляющую конец альтернативного пути, начинающегося префиксом, общим для всех ребер из v.
Обновление суффиксных ссылок
После каждого расширения производится специальный проход по только что созданным внутренним вершинам для обновления их суффиксных ссылок соответствующим образом. Это позволяет поддерживать корректность структуры и гарантировать линейное общее время.
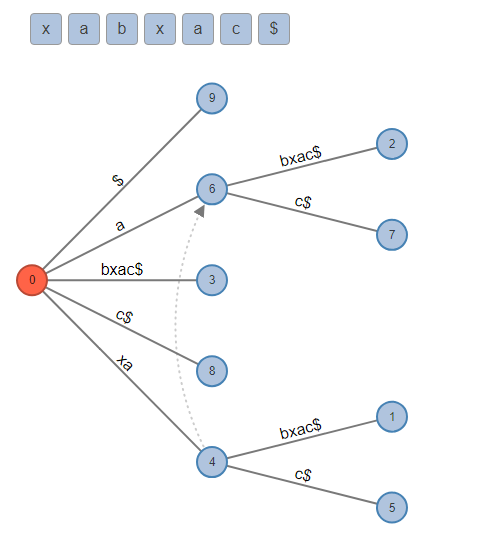
Пример
Рассмотрим построение
суффиксного дерева для строки S = "xabxac" с помощью алгоритма
Укконена:
- Пустое дерево
- Фаза 1 ('x'): создание листа x
- Фаза 2 ('a'): добавление a к x -> xa, новый лист a
- Фаза 3 ('b'): xa -> xab, a -> ab, новый лист b
- Фаза 4 ('x'): xab -> xabx, ab -> bx, b -> x (правило 3)
- Фаза 5 ('a'): xabx-> xabxa, bx -> bxa, xa (правило 3)
- Фаза 6 ('c'): xabxa -> xabxac, bxa -> bxac, a -> ac, новый лист c
Итоговое дерево компактно представляет все суффиксы строки:
Публикации и ресурсы
Реализации алгоритма Укконена посвящено множество публикаций. Все началось с поста на Stack Overflow, в котором разработчики делились сложностями, объяснениями, и попытками реализации алгоритма. Построение суффиксного дерева методом Укконена быстро стало одной из самых популярных тем на Stack Overflow, а реализация алгоритма на том или ином языке – одним из профессиональных вызовов для продвинутых разработчиков.
Вот что стоит почитать и посмотреть на тему алгоритма Укконена:
- Тот самый пост на Stack Overflow, в комментарии к которому пользователь jogojapan в 2012 году изложил основные концепции построения суффиксного дерева.
- Перевод этого комментария на Хабре.
- Анимированная визуализация процесса создания суффиксного дерева.
- Видео с объяснением алгоритма.
- Пост автора одной из немногих полных реализаций алгоритма (на Python 2). По словам разработчика, впервые в жизни ему пришлось нарисовать блок-схему, чтобы наконец-то разобраться в работе алгоритма:
- Самое полное математическое объяснение и доказательство алгоритма – в книге Дэна Гасфилда «Строки, деревья и последовательности в алгоритмах» (Algorithms on strings, trees, and sequences: computer science and computational biology, Dan Gusfield).
Реализация алгоритма Укконена на Python
В ходе реализации алгоритма построения суффиксного дерева нужно учитывать множество деталей для корректной обработки различных ситуаций. Подробнее всего эти тонкости изложены здесь.
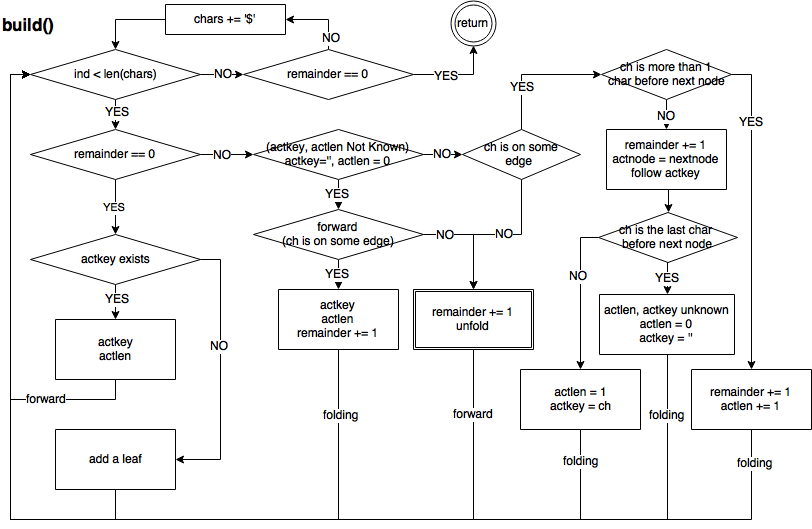
Главная функция
Функция main() управляет основным потоком построения суффиксного дерева, в соответствии с приведенной выше блок-схемой:
- Процесс начинается в верхнем левом углу диаграммы.
- В блоках принятия решений выполняются проверки специальных случаев и условий.
- Операции перемещения, развертывания, разделения и обработки суффиксных ссылок вынесены в отдельные функции.
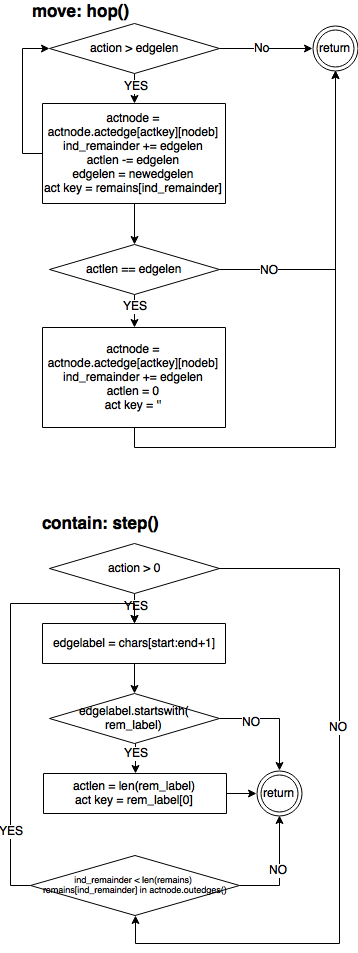
Перемещение
Прыжки – функция hop() – используются, когда нужно перейти от текущего узла к следующему узлу операции. Переход от узла к узлу выполняется вдоль ребер.
Шаги – функция step() применяются, когда активный узел верен, но операция должна быть выполнена посередине ребра. Переход по символам к нужной позиции также выполняется вдоль ребра.
Развертывание
Операция развертывания – функция unfold() – запускается, как только мы встречаем новый символ, отличающийся от предыдущих. При развертывании в дереве создается новое ребро для оставшейся части строки.
Процесс развертывания обрабатывает различные ситуации, когда остаток строки исчерпан или нет, и устанавливает суффиксные ссылки для новых узлов, разбивая ребра при необходимости.
Важные наблюдения:
1. В зависимости от длины цепочки суффиксных ссылок может потребоваться один или несколько циклов развертывания.
2. Если строка не заканчивается уникальным символом, добавляется специальный символ $.
3. Развертывание прекращается в двух случаях:
- Ситуация 1: Оставшаяся строка исчерпана
Если (цепочка суффикс-ссылок исчерпана, но остаток строки еще не исчерпан):
Перейти к корневому узлу,
получить actkey, укоротив остаток на 1 символ с начала,
перезапустить процесс,
Повторять до тех пор, пока остаток строки не будет исчерпан.
Если (остаток строки исчерпан до исчерпания суффикс-ссылок):
Завершить процесс.
- Ситуация 2: Оставшаяся строка не исчерпана
Если остаток строки полностью находится внутри пути, и
на этом пути не найдено отличающихся символов,
а исходная строка не была исчерпана в процессе наращивания вперед:
Сохранить остаток,
Продвинуться вперед, чтобы найти другой отличающийся символ из исходной строки,
начиная с текущего actnode, вдоль actkey,
изменить actlength, REMAINS и ind_remain соответственно.
Если остаток перестанет уменьшаться,
завершить текущий процесс развертывания
(что означает прекратить добавление суффикс-ссылок для разбиения ребер на этом шаге).
Если остаток строки полностью находится внутри пути, и
исходная строка исчерпана этим остатком:
Если эту строку невозможно завершить:
добавить зарезервированный символ, например '$', для завершения.
Если остаток строки перестает увеличиваться:
завершить этот шаг,
прекратить добавление суффикс-ссылок для текущего шага.
Разбиение
Процесс разбиения ребра – функция split() – необходим для поддержания инвариантов суффиксного дерева, когда новый символ не может быть добавлен к существующей ветви. Разбиение позволяет создавать новые узлы и ребра, чтобы отражать все уникальные суффиксы в дереве. В зависимости от положения actkey (активного ключа), разбиение может произойти либо на узле, либо на ребре.
На узле:
- Если текущий символ в остатке строки REMAINS не совпадает ни с одним из исходящих ребер из текущего узла actnode, то создается новая ветвь (новый лист).
- Переменные actnode, actlength (длина активного ребра), actkey, REMAINS и ind_remain (индекс остатка) обновляются соответствующим образом.
На ребре:
- Если текущий символ в остатке строки не совпадает с символом на активном ребре actkey, то происходит разбиение ребра.
- Создается новый узел в середине ребра.
- Исходное ребро разбивается на два ребра: от родительского узла до нового узла и от нового узла до конца исходного ребра.
- Добавляется новая ветвь (лист) из нового узла с меткой, соответствующей остатку строки.
- Переменные actnode, actlength, actkey, REMAINS и ind_remain обновляются соответствующим образом.
Суффиксные ссылки
Суффиксные ссылки играют важную роль: они связывают узлы, представляющие суффиксы строки, и помогают эффективно перемещаться по дереву при его построении. Перечисленные ниже правила и наблюдения гарантируют, что суффиксные ссылки устанавливаются корректно, позволяя алгоритму обрабатывать различные ситуации во время разворачивания дерева и добавления новых символов.
Правило 1
Если после вставки из actnode == root, а actlength > 0, то: actnode = root, actlength -= 1, ind_remain += 1, actkey = REMAINS[ind_remain].
Правило 2
Если мы разбиваем ребро или добавляем лист во внутреннем узле, и текущий actnode не является первым расширенным узлом в этом раунде процесса развертывания, связываем предыдущий actnode с этим actnode с помощью суффиксной ссылки.
Правило 3
После расширения (либо разбиения ребра, либо только добавления листа) в actnode != root, следуем по суффикс-ссылке и устанавливаем actnode = suffixlink. Если suffixlink равен None, устанавливаем actnode = root. В любом случае actlength и actedge остаются неизменными.
Код построения суффиксного дерева на Python
С учетом всех изложенных наблюдений и правил код алгоритма Укконена выглядит так:
class Node:
# Статическая переменная для нумерации узлов
__num__ = -1
def __init__(self, parent_key, out_edges, suffix_link=None):
# Ключ родительского узла
self.parent_key = parent_key
# Словарь исходящих ребер узла
self.out_edges = out_edges
# Суффиксная ссылка
self.suffix_link = suffix_link
# Увеличиваем счетчик узлов и присваиваем уникальный идентификатор
Node.__num__ += 1
self.id = Node.__num__
def get_out_edges(self):
return self.out_edges
def set_out_edge(self, key, anode, label_start, label_end, bnode):
# Добавление исходящего ребра к узлу
self.out_edges = self.out_edges or {}
self.out_edges[key] = (anode, label_start, label_end, bnode)
def get_out_edge(self, key):
return self.out_edges.get(key, None)
def get_parent_key(self):
return self.parent_key
def set_parent_key(self, parent_key):
self.parent_key = parent_key
def get_suffix_link(self):
return self.suffix_link
def set_suffix_link(self, node):
self.suffix_link = node
def get_id(self):
return self.id
@staticmethod
def __draw__(root_node, chars, v, ed='#'):
# Рекурсивный метод для отрисовки дерева
# Разделение исходящих ребер на те, которые ведут к узлам без детей, и те, которые ведут к узлам с детьми
edges = root_node.get_out_edges().items()
no_gc, has_gc = [], []
for edge in edges:
if edge[1][3].get_out_edges() is None:
no_gc.append(edge)
else:
has_gc.append(edge)
# Порядок отрисовки ребер: сначала ребра к узлам с детьми, затем ребра к листьям
gc = has_gc + no_gc if v == 0 else no_gc + has_gc
maxlen = len(chars) + 6
for k, (parent, s, t, node) in gc:
# Если конец ребра не указан, устанавливаем его как длину строки или специальный символ
if t == '#':
t = len(chars) if ed == '#' else ed
linkid = ''
# Добавляем суффиксную ссылку, если она существует
if node.get_suffix_link() is not None:
linkid = '->' + str(node.get_suffix_link().get_id())
# Отрисовка ребра и рекурсивный вызов для его потомков
if v == 0:
print(f'{" " * maxlen * v}|\n'
f'{" " * maxlen * v}|{" " * 3}{chars[s:t + 1]}\n'
f'+{" " * maxlen * v}-{"-" * (maxlen - 1)}● ({str(node.get_id()) + linkid})')
else:
print(f'|{" " * maxlen * v}|\n'
f'|{" " * maxlen * v}|{" " * 3}{chars[s:t + 1]}\n'
f'|{" " * maxlen * v}+{"-" * (maxlen - 1)}● ({str(node.get_id()) + linkid})')
if node.get_out_edges():
Node.__draw__(node, chars, v + 1, ed)
@staticmethod
def draw(root, chars, ed='#'):
# Запуск отрисовки дерева, начиная с корневого узла
print(f'\n{chars}\n● (0)')
Node.__draw__(root, chars, 0, ed)
def build(chars, regularize=False):
# Построение дерева суффиксов из строки chars
root = Node(None, None, None) # Создание корневого узла
act_node = root # Текущий узел
act_key = '' # Текущий ключ (первый символ ребра)
act_len = 0 # Длина текущего ребра
remainder = 0 # Остаток строки для обработки
ind = 0 # Индекс обрабатываемого символа
while ind < len(chars):
ch = chars[ind]
if remainder == 0:
# Если остаток равен 0, проверяем, существует ли исходящее ребро с символом ch
if act_node.get_out_edges() and ch in act_node.get_out_edges():
act_key = ch
act_len = 1
remainder = 1
anode, start, end, bnode = act_node.get_out_edge(act_key)
if end == '#':
end = ind
if end - start + 1 == act_len:
act_node = bnode
act_key = ''
act_len = 0
else:
# Если ребра не существует, создаем новый лист
leaf = Node(None, None, None)
act_node.set_out_edge(chars[ind], act_node, ind, '#', leaf)
leaf.set_parent_key((act_node, chars[ind]))
else:
if not act_key and not act_len:
# Если мы на узле, проверяем, существует ли исходящее ребро с символом ch
if ch in act_node.get_out_edges():
act_key = ch
act_len = 1
remainder += 1
else:
# Если ребра не существует, разворачиваем дерево
remainder += 1
remainder, act_node, act_key, act_len = unfold(root, chars, ind, remainder, act_node, act_key, act_len)
else: # compare on edge
# Если мы на ребре, проверяем, совпадают ли символы на ребре и в остатке строки
out_edge = act_node.get_out_edge(act_key)
if out_edge:
anode, start, end, bnode = out_edge
if end == '#':
end = ind
compare_pos = start + act_len
if chars[compare_pos] != ch:
# Если символы не совпадают, разворачиваем дерево
remainder += 1
remainder, act_node, act_key, act_len = unfold(root, chars, ind, remainder, act_node, act_key, act_len)
else:
if compare_pos < end: # on edge
# Если мы все еще на ребре, увеличиваем длину ребра
act_len += 1
remainder += 1
else:
# Если мы достигли конца ребра, переходим к следующему узлу
remainder += 1
act_node = bnode
if compare_pos == end:
act_len = 0
act_key = ''
else:
act_len = 1
act_key = ch
ind += 1
if ind == len(chars) and remainder > 0:
# Если мы обработали всю строку, но остаток не равен 0, добавляем специальный символ
if regularize:
chars += '$'
return root, chars
def unfold(root, chars, ind, remainder, act_node, act_key, act_len):
# Вспомогательная рекурсивная функция для разворачивания дерева
pre_node = None
while remainder > 0:
remains = chars[ind - remainder + 1:ind + 1]
act_len_re = len(remains) - 1 - act_len
act_node, act_key, act_len, act_len_re = hop(ind, act_node, act_key, act_len, remains, act_len_re)
lost, act_node, act_key, act_len, act_len_re = step(chars, ind, act_node, act_key, act_len, remains, act_len_re)
if lost:
# Если мы потеряли путь в дереве, устанавливаем суффиксную ссылку и выходим из функции
if act_len == 1 and pre_node is not None and act_node is not root:
pre_node.set_suffix_link(act_node)
return remainder, act_node, act_key, act_len
if not act_len:
# Если мы на узле и символ не совпадает с ребром, создаем новый лист
if remains[act_len_re] not in act_node.get_out_edges():
leaf = Node(None, None, None)
act_node.set_out_edge(remains[act_len_re], act_node, ind, '#', leaf)
leaf.set_parent_key((act_node, remains[act_len_re]))
else:
# Если мы на ребре, проверяем, совпадают ли символы
out_edge = act_node.get_out_edge(act_key)
if out_edge:
anode, start, end, bnode = out_edge
if remains[act_len_re + act_len] != chars[start + act_len]:
# Если символы не совпадают, разбиваем ребро
new_node = Node(None, None, None)
act_node.set_out_edge(act_key, act_node, start, start + act_len - 1, new_node)
new_node.set_parent_key((act_node, act_key))
new_node.set_out_edge(chars[start + act_len], new_node, start + act_len, end, bnode)
leaf = Node(None, None, None)
new_node.set_out_edge(chars[ind], new_node, ind, '#', leaf)
leaf.set_parent_key((new_node, chars[ind]))
else:
return remainder, act_node, act_key, act_len
# Устанавливаем суффиксную ссылку для нового узла
if pre_node and 'leaf' in locals() and leaf.get_parent_key()[0] is not root:
pre_node.set_suffix_link(leaf.get_parent_key()[0])
if 'leaf' in locals() and leaf.get_parent_key()[0] is not root:
pre_node = leaf.get_parent_key()[0]
# Переходим к следующему узлу по суффиксной ссылке или к корневому узлу
if act_node == root and remainder > 1:
act_key = remains[1]
act_len -= 1
if act_node.get_suffix_link() is not None:
act_node = act_node.get_suffix_link()
else:
act_node = root
remainder -= 1
return remainder, act_node, act_key, act_len
def step(chars, ind, act_node, act_key, act_len, remains, ind_remainder):
# Вспомогательная функция для переходов по ребрам и узлам дерева
rem_label = remains[ind_remainder:]
if act_len > 0:
# Если мы на ребре, проверяем, совпадает ли остаток строки с меткой ребра
out_edge = act_node.get_out_edge(act_key)
if out_edge:
anode, start, end, bnode = out_edge
if end == '#':
end = ind
edge_label = chars[start:end + 1]
if edge_label.startswith(rem_label):
act_len = len(rem_label)
act_key = rem_label[0]
return True, act_node, act_key, act_len, ind_remainder
else:
# Если мы на узле, проверяем, существует ли исходящее ребро с символом из остатка строки
if ind_remainder < len(remains) and remains[ind_remainder] in act_node.get_out_edges():
out_edge = act_node.get_out_edge(remains[ind_remainder])
if out_edge:
anode, start, end, bnode = out_edge
if end == '#':
end = ind
edge_label = chars[start:end + 1]
if edge_label.startswith(rem_label):
act_len = len(rem_label)
act_key = rem_label[0]
return True, act_node, act_key, act_len, ind_remainder
return False, act_node, act_key, act_len, ind_remainder
def hop(ind, act_node, act_key, act_len, remains, ind_remainder):
# Вспомогательная функция для перехода по ребру дерева
out_edge = act_node.get_out_edge(act_key)
if not out_edge or (not act_len and not act_key):
return act_node, act_key, act_len, ind_remainder
anode, start, end, bnode = out_edge
if end == '#':
end = ind
edge_length = end - start + 1
while act_len > edge_length:
# Переходим к следующему узлу по ребру, если длина ребра меньше, чем act_len
act_node = bnode
ind_remainder += edge_length
act_key = remains[ind_remainder]
act_len -= edge_length
out_edge = act_node.get_out_edge(act_key)
if out_edge:
anode, start, end, bnode = out_edge
if end == '#':
end = ind
edge_length = end - start + 1
else:
act_key = ''
act_len = 0
break
if act_len == edge_length:
act_node = bnode
act_key = ''
act_len = 0
ind_remainder += edge_length
return act_node, act_key, act_len, ind_remainder
if __name__ == "__main__":
st = input("Введите строку: ")
tree, pst = build(st, regularize=True)
Node.draw(tree, pst, ed='#')
А это суффиксное дерево строки программирование:
программирование
● (0)
|
| р
+----------------------● (5)
| |
| | аммирование
| +---------------------● (6)
| |
| | о
| +---------------------● (12->14)
| |
| | граммирование
| +---------------------● (2)
| |
| | вание
| +---------------------● (13)
|
| о
+----------------------● (14)
| |
| | граммирование
| +---------------------● (3)
| |
| | вание
| +---------------------● (15)
|
| а
+----------------------● (17)
| |
| | ммирование
| +---------------------● (7)
| |
| | ние
| +---------------------● (18)
|
| м
+----------------------● (9)
| |
| | мирование
| +---------------------● (8)
| |
| | ирование
| +---------------------● (10)
|
| и
+----------------------● (20)
| |
| | рование
| +---------------------● (11)
| |
| | е
| +---------------------● (21)
|
| программирование
+----------------------● (1)
|
| граммирование
+----------------------● (4)
|
| вание
+----------------------● (16)
|
| ние
+----------------------● (19)
|
| е
+----------------------● (22)
Подведем итоги
Алгоритм Укконена – элегантное решение для построения суффиксного дерева строки за линейное время. Ключевым моментом здесь является использование неявного суффиксного дерева – компактного представления, которое позволяет избежать избыточного дублирования вершин. Благодаря эффективным техническим приемам – суффиксным ссылкам и точкам продолжения, – алгоритм обновляет неявное суффиксное дерево на каждой итерации, добавляя новый символ строки.
Хотя реализация алгоритма кажется непростой на первый взгляд, вникнуть в него стоит: этот оригинальный подход к построению деревьев может обеспечить идеальное решение многих сложных задач, связанных с обработкой строк.


Комментарии