Момент настал – вы переезжаете в Сан-Франциско, чтобы стать известным дата сайентистом. Будете работать в крупной компании и скоро прославитесь. Но не всё сразу. Поначалу придётся ютиться в жилище, много меньшем, чем нынешний дом. Нужно решить, что взять с собой. Вы аналитик и намерены решить задачу эффективно. Обсудим алгоритм?
Описание проблемы
Представим, что на данный момент вы живёте в довольно большой квартире площадью 100 м2, а вещи занимают 50 м2. Вы знаете, что площадь нового жилья составит 40 м2 и хотите, чтобы вещи занимали не более 20 м2. Вы любите, когда на полу есть свободное место, да и не всё можно поставить впритык друг к другу. Нужно составить список вещей, определить площадь, занимаемую каждой вещью и составить рейтинг ценности предметов. Конечная цель – максимизировать материальную ценность того, что разместится на 20 квадратных метрах.
Перечисляем предметы
Вы составили список вещей и выразили занимаемую площадь в квадратных дециметрах (1 дм2 = 0.01 м2). Каждому предмету сопоставили ценность по шкале от 0 до 100. Получилась сводка данных о 29 предметах, которую можно оформить как словарь вида {'название предмета':(площадь, ценность) }:
stuffdict = {'couch_s':(300,75),
'couch_b':(500,80),
'bed':(400,100),
'closet':(200,50),
'bed_s':(200,40),
'desk':(200,70),
'table':(300,80),
'tv_table':(200,30),
'armchair':(100,30),
'bookshelf':(200,60),
'cabinet':(150,20),
'game_table':(150,30),
'hammock':(250,45),
'diner_table_with_chairs':(250,70),
'stools':(150,30),
'mirror':(100,20),
'instrument':(300,70),
'plant_1':(25,10),
'plant_2':(30,20),
'plant_3':(45,25),
'sideboard':(175,30),
'chest_of_drawers':(25,40),
'guest_bed':(250,40),
'standing_lamp':(20,30),
'garbage_can':(30,35),
'bar_with_stools':(200,40),
'bike_stand':(100,80),
'chest':(150,25),
'heater':(100,25)
}
Готово! Теперь видно, что кровать ('bed') занимает 400 дм2, а её ценность составляет 100, игровой стол ('game_table') занимает 150 дм2 квадратных метра и имеет ценность 30.
Максимизация ценности
Как максимизировать суммарную ценность объектов так, чтобы суммарная площадь не превышала 2000 дм2? Можно попробовать перебрать все возможные комбинации и рассчитать суммарную ценность для каждой из комбинаций. Решение получится, если выбрать максимальную суммарную ценность для 2000 дм2. Но вот незадача: и комбинаторика, и теория множеств утверждают, что 29 предметов дают 2²⁹ возможных комбинаций выбора предметов.
То есть более 536 миллионов. Похоже, такой перебор займёт некоторое время. Нельзя ли быстрее?
Стоит подумать о других вариантах. Что если начать с наиболее ценного предмета, затем следующего за ним по ценности, и так до тех пор, пока не заполнятся 20 квадратных метров? Такой алгоритм явно быстрее. Но даст ли он оптимальное решение? Есть сомнения. Как быстро решить задачу и найти лучшее решение?
Примечание: описанные выше случаи соответствуют полному перебору (метод «грубой силы», англ. brute force) и жадному (англ. greedy) алгоритму.
Динамическое программирование
Соответствующий класс проблем называют задача о рюкзаке. Своё название проблема получила от конечной цели: уложить как можно большее число ценных вещей в рюкзак при условии, что вместимость рюкзака ограничена. В общем виде задачу можно сформулировать так: из заданного множества предметов со свойствами «стоимость» и «вес» требуется отобрать подмножество с максимальной полной стоимостью, соблюдая при этом ограничение на суммарный вес.
К счастью, знакомый слышал об этом классе задач и подсказал вам более разумный способ справиться с проблемой. Он объяснил, что можно рекурсивно разделить проблему на более мелкие подзадачи. Сохраняя результаты в ячейках таблицы мемоизации и используя их на следующих итерациях, вы быстро найдёте оптимальное решение. Вы как бы обменяете программную память на время. То есть воспользуетесь методом динамического программирования.
Этапы решения задачи с помощью динамического программирования
- Создаём словарь со списком элементов и их параметрами (площадь, ценность).
- Создаём списки значений площади и ценности.
- Используем списки для построения таблиц мемоизации.
- Получаем элементы из последней строки таблицы. Последняя строка таблицы мемоизации содержит оптимальное решение. Возможно, существует несколько оптимальных решений. Например, когда есть два предмета с одинаковой площадью и стоимостью или ряд предметов имеют суммарные площадь и ценность, как у другого предмета.
Рассмотрим, как реализовать этот план на практике. Первый шаг мы предусмотрительно выполнили ранее, перейдём ко второму.
Создаём списки значений площади и ценности
Разделяем списки значений исходного словаря, например, так:
def get_area_and_value(stuffdict):
area = [stuffdict[item][0] for item in stuffdict]
value = [stuffdict[item][1] for item in stuffdict]
return area, value
Используем списки для мемоизации
Пусть n – общее число предметов, A – их максимально допустимая суммарная площадь в новом жилище (2000 дм2). Составим таблицу из n + 1 строк и A + 1 столбцов. Строки пронумеруем индексом i, столбцы – индексом a (чтобы помнить что в столбцах площадь, area). То есть в качестве номеров столбцов мы рассматриваем дискретные значения площади, отличающиеся друг от друга на 1.
def get_memtable(stuffdict, A=2000):
area, value = get_area_and_value(stuffdict)
n = len(value) # находим размеры таблицы
# создаём таблицу из нулевых значений
V = [[0 for a in range(A+1)] for i in range(n+1)]
for i in range(n+1):
for a in range(A+1):
# базовый случай
if i == 0 or a == 0:
V[i][a] = 0
# если площадь предмета меньше площади столбца,
# максимизируем значение суммарной ценности
elif area[i-1] <= a:
V[i][a] = max(value[i-1] + V[i-1][a-area[i-1]], V[i-1][a])
# если площадь предмета больше площади столбца,
# забираем значение ячейки из предыдущей строки
else:
V[i][a] = V[i-1][a]
return V, area, value
Вначале создаётся и заполняется таблица в виде вложенных списков. Нулевую строку и нулевой столбец заполняем нулями. Это базовый случай: когда площадь или количество элементов равны нулю, значение ячейки равно нулю. Далее таблица значений V будет заполняться строка за строкой слева направо и сверху вниз:
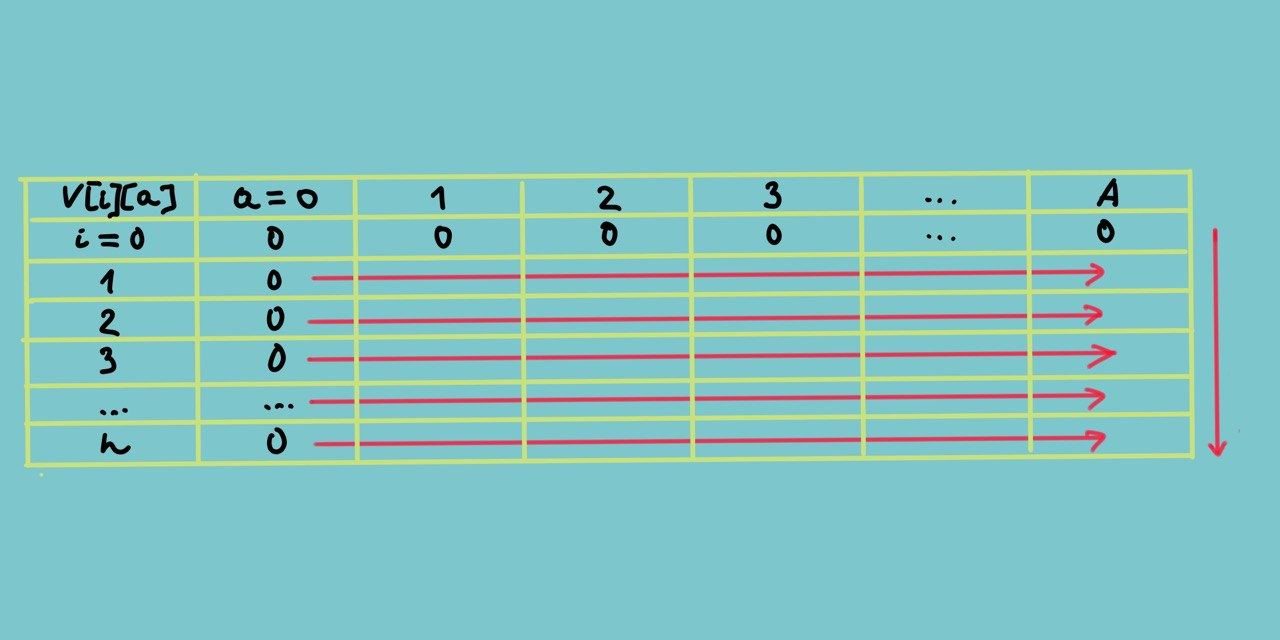
Если площадь текущего элемента меньше или равна площади (номеру столбца) текущей ячейки, вычисляем значение ячейки следуя правилу:
V[i][a] = max(value[i-1] + V[i-1][a-area[i-1]], V[i-1][a])
То есть выбираем максимальное из двух значений:
- Сумма ценности текущего предмета
value[i-1]и величины элемента из предыдущей строкиi-1с площадью, меньшей на величину площади текущего предметаarea[i-1]. Обратите внимание: нужно помнить, что элементы в таблице отличаются по нумерации на единицу из-за нулевой строки. - Значение элемента предыдущей строки с той же площадью, то есть из того же столбца, что текущая ячейка. То же значение устанавливается в случае, если площадь текущей ячейки меньше, чем площадь текущего элемента (см. блок
else)
За счёт такого подхода при одной и той же суммарной площади элементов происходит максимизация суммарной ценности.
Забираем нужные элементы из последней строки таблицы
Найдём набор предметов с максимальной суммарной ценностью для указанной возможной площади. Начнём с нижнего правого угла таблицы с максимальным значением, и соберём предметы:
def get_selected_items_list(stuffdict, A=2000):
V, area, value = get_memtable(stuffdict)
n = len(value)
res = V[n][A] # начинаем с последнего элемента таблицы
a = A # начальная площадь - максимальная
items_list = [] # список площадей и ценностей
for i in range(n, 0, -1): # идём в обратном порядке
if res <= 0: # условие прерывания - собрали "рюкзак"
break
if res == V[i-1][a]: # ничего не делаем, двигаемся дальше
continue
else:
# "забираем" предмет
items_list.append((area[i-1], value[i-1]))
res -= value[i-1] # отнимаем значение ценности от общей
a -= area[i-1] # отнимаем площадь от общей
selected_stuff = []
# находим ключи исходного словаря - названия предметов
for search in items_list:
for key, value in stuffdict.items():
if value == search:
selected_stuff.append(key)
return selected_stuff
Итак, мы нашли список:
>>> stuff = get_selected_items_list(stuffdict)
>>> print(stuff)
['bike_stand', 'garbage_can', 'standing_lamp', 'chest_of_drawers',
'plant_3', 'plant_2', 'diner_table_with_chairs', 'bookshelf',
'armchair', 'table', 'desk', 'bed', 'couch_s']
Проверим суммарные площадь и ценность собранных предметов:
>>> totarea = sum([stuffdict[item][0] for item in stuff])
>>> totvalue = sum([stuffdict[item][1] for item in stuff])
>>> print(totarea)
2000
>>> print(totvalue)
715
Получилось! Собираем вещи и отправляемся в путь (звучит песня Mamas & Paps – San Francisco).
Бонус: Тепловая карта таблицы
Тепловая карта ниже отображает рассмотренную выше таблицу. По оси абсцисс отложена доступная площадь, по оси ординат – список предметов. Цветовая шкала соответствует суммарной ценности. Можно видеть, как значения возрастают по мере продвижения по таблице снизу вверх.
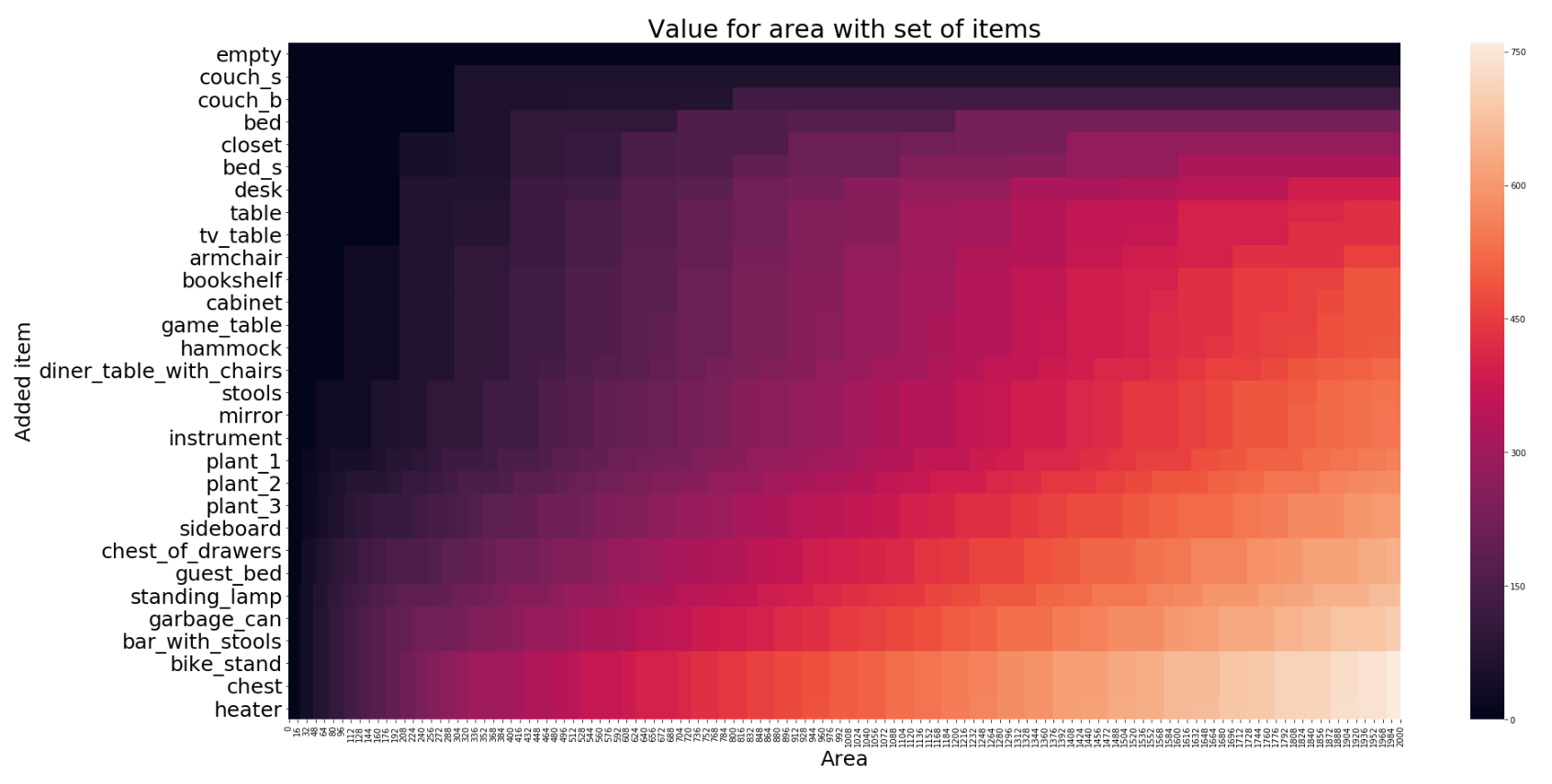
Для построения использовалась библиотека matplotlib:
def plot_memtable(V, stuffdict):
plt.figure(figsize=(30,15))
item_list = list(stuffdict.keys())
item_list.insert(0, 'empty')
sns.heatmap(V, yticklabels=item_list)
plt.yticks(size=25)
plt.xlabel('Area', size=25)
plt.ylabel('Added item', size=25)
plt.title('Value for Area with Set of Items', size=30)
plt.show()
А тем, кто следит за нашим сериалом головоломок, динамическое программирование также поможет решить текущую задачу (головоломку о беглеце).




Комментарии