Динамическое программирование – мощный метод решения сложных задач путем их разбиения на более простые подзадачи. Этот алгоритмический подход, впервые предложенный математиком Ричардом Беллманом в 1950-х годах, произвел революцию в области оптимизации и нашел применение в самых разных областях – от биоинформатики до экономики.
С точки зрения разделения исходной задачи на комбинацию мелких подзадач ДП похоже на метод разделяй и властвуй. Однако ключевое отличие ДП в том, что одна и та же подзадача может возникать многократно. Поэтому для повышения эффективности ДП важно сохранять результаты промежуточных вычислений (кэшировать их).
Чтобы проиллюстрировать идею ДП, рассмотрим задачу вычисления чисел Фибоначчи. Первые два числа Фибоначчи – 0 и 1. Последующие числа являются суммами двух предыдущих чисел, формируя последовательность 0, 1, 1, 2, 3, 5, 8, 13, 21, ... Числа Фибоначчи используются во многих различных областях — от биологии до анализа структур данных и параллельных вычислений.
Математически n-е число Фибоначчи F(n) задается уравнением F(n) = F(n-1) + F(n-2), где F(0) = 0 и F(1) = 1. Функция, которая вычисляет F(n) рекурсивно, вызывает саму себя, и ее временная сложность экспоненциально растет с увеличением n. Это происходит из-за того, что рекурсивная функция многократно вычисляет одни и те же значения F(n):

Кэширование промежуточных результатов делает временную сложность вычисления n-го числа Фибоначчи линейной по n, хотя и за счет использования O(n) памяти:
def fibonacci(n, cache={}):
if n <= 1:
return n
elif n not in cache:
cache[n] = fibonacci(n - 1) + fibonacci(n - 2)
return cache[n]
Минимизация объема кэша — один из самых важных аспектов динамического программирования. Чтобы минимизировать использование памяти, можно использовать итеративный подход, начиная с первых двух чисел Фибоначчи и постепенно вычисляя последующие. Этот подход позволяет переиспользовать память, храня только последние два вычисленных числа: временная сложность останется прежней — O(n), а пространственная улучшится до O(1):
def fibonacci(n):
if n <= 1:
return n
f_minus_2, f_minus_1 = 0, 1
for _ in range(2, n + 1):
f = f_minus_2 + f_minus_1
f_minus_2, f_minus_1 = f_minus_1, f
return f_minus_1
Основные принципы и сложности динамического программирования
Пример с вычислением ряда Фибоначчи демонстрирует главный принцип ДП — необходимо найти такой способ разделения исходной задачи на подзадачи, чтобы выполнялись два важных условия:
- Комбинация готовых решений подзадач максимально упрощает решение исходной задачи.
- Решения подзадач можно эффективно кэшировать так, чтобы не перегружать память.
Основная сложность ДП заключается в идентификации подзадач: бывают ситуации, когда нахождение правильного способа декомпозиции требует глубокого анализа задачи и нетривиального подхода к разделению решения.
Рассмотрим более сложный пример использования ДП — в заданном массиве целых чисел найдем подмассив с максимальной суммой элементов. Например, в массиве [904,
40, 523, 12, -335, -385, -124, 481, -31] максимальный подмассив начинается с
индекса 0 и заканчивается индексом 3, и имеет сумму 1479:

Сложность возможных решений выглядит так:
- Брутфорсный подход вычисляет
сумму для каждого возможного подмассива и имеет сложность O(n³), потому что число возможных подмассивов равно n∗(n+1)/2 => (O(n2)), а вычисление суммы занимает O(n). В итоге O(n2) * O(n) = O(n3).
- Улучшенный подход имеет сложность O(n2) за счет предварительного расчета суммы префиксов и использования памяти O(n). Нужно вычислить такой массив s, чтобы s[k] был равен сумме элементов с индексами от 0 до k-1. Для каждого подмассива A[i..j] сумма будет равна s[j+1] – s[i].
- Разделяй и властвуй имеет сложность O(n log n), поскольку рекурсивно делит массив пополам и объединяет решения.
Решить эту задачу за время O(n) и с использованием памяти О(1) можно только при помощи динамического программирования, итеративно вычисляя максимальную сумму. Приведенное ниже решение известно как алгоритм Кадане:
- Вместо того, чтобы перебирать все возможные подмассивы и вычислять их суммы, мы эффективно отслеживаем максимальную сумму подмассива, заканчивающегося в текущей позиции.
- Если текущая частичная сумма меньше минимальной встреченной ранее, то начало максимального подмассива может находиться после этой минимальной суммы. Вычитая минимальную сумму из текущей, мы получаем максимальную возможную сумму подмассива, заканчивающегося текущим элементом.
- Если в массиве нет положительных элементов, решением считается число, максимально близкое к 0. Например, для массива [-335, -385, -124, -6, -31] решением будет -6.
def find_maximum_subarray(A):
if not A:
return "Массив пуст"
max_sum = float('-inf')
current_sum = 0
for x in A:
current_sum = max(x, current_sum + x)
max_sum = max(max_sum, current_sum)
return max_sum
A = [904, 40, 523, 12, -335, -385, -124, 481, -31]
result = find_maximum_subarray(A)
print(f"Максимальная сумма подмассива: {result}")
Результат:
Максимальная сумма подмассива: 1479
Как и когда использовать динамическое программирование
ДП подходит для решения следующих типов задач:
- Оптимизация — нахождение максимального или минимального значения.
- Подсчет — например, подсчет количества различных вариантов достижения какой-либо цели.
- Принятие решений — выбор наилучшего решения из нескольких вариантов.
Важные моменты:
- Рекурсия и итерация. ДП можно реализовать как рекурсивно, так и итеративно. Иногда рекурсия эффективнее итеративного подхода, например, когда решение можно найти быстро или есть возможность сократить количество подзадач с помощью отсечения. При этом кэш чаще всего строится снизу вверх, то есть итеративно.
- Использование кэша. Когда ДП реализуется рекурсивно, кэш обычно представляет собой динамическую структуру данных — хеш-таблицу или двоичное дерево поиска. При итеративной реализации кэш чаще всего представляет собой одномерный или многомерный массив. В целях оптимизации место в кэше можно освободить, если известно, что конкретные данные больше не потребуются.
- Распространенная ошибка — попытка разделить задачу на две равные половины, как в алгоритме быстрой сортировки. В большинстве случаев такое разделение не приводит к оптимальному решению.
- ДП не универсально — не каждую задачу оптимизации можно решить с его помощью. Например, в задаче о поиске самого длинного пути между городами без повторения промежуточных городов, оптимальные подпути могут не быть частью оптимального общего пути.
Как щелкать задачки как орешки?
Знаешь, в играх есть супероружие, которое делает тебя непобедимым. Так вот, курс «Алгоритмы и структуры данных» – что-то типа такого супероружия для программистов. После него сложные задачи разносишь в пух и прах! 🥜💥🔨
На курсе ты:
- Узнаешь о популярных алгоритмах и структурах данных
- Получишь практический опыт решения сложных алгоритмических задач
- Научишься писать более короткий и эффективный код
Примеры задач, которые эффективнее всего решаются с помощью ДП
Задача 1: Американский футбол
В американском футболе каждое действие может привести к разному количеству очков: 2 очка (сэйфти), 3 очка (филд-гол) или 7 очков (тачдаун). Существует множество различных комбинаций из этих 2, 3 и 7 очков, которые могут составить итоговый счет. Например, для достижения счета 12 есть четыре возможные комбинации:
- 6 сэйфти (2 x 6 = 12)
- 3 сэйфти и 2 филд-гола (2 x 3 + 3 x 2 = 12)
- 1 сэйфти, 1 филд-гол и 1 тачдаун (2 x 1 + 3 x 1 + 7 x 1 = 12)
- 4 филд-гола (3 x 4 = 12)
Нужно написать программу, которая принимает итоговый счет и доступные значения очков за отдельные действия, и возвращает количество возможных комбинаций действий, приводящих к этому счету.
Решение
На примере разбора небольшого итогового счета можно интуитивно понять, как достичь нужного значения. Например, итоговый счет 9 можно получить так:
- Набрать сначала 7 очков, затем 2 очка.
- Набрать сначала 6 очков, затем 3 очка.
- Набрать сначала 2 очка, затем 7 очков.
Обобщая это наблюдение, можно сказать, что любой счет s можно получить, если сначала получить s – 2 очков и добавить к ним 2 очка, либо получить s – 3 очков и добавить 3 очка, либо получить s – 7 очков и добавить 7 очков. Этот принцип можно использовать для рекурсивного вычисления всех возможных последовательностей действий, приводящих к нужному счету.
Однако рекурсивный перебор всех последовательностей может быть очень затратным по времени. Вместо этого лучше использовать динамическое программирование. Для этого мы создаем двумерный массив A, где A[i][j] хранит количество комбинаций, которые дают итоговый счет j, используя первые i типов игровых действий. Например, A[1][12] будет хранить количество способов набрать 12 очков, используя действия на 2 и 3 очка:

Чтобы заполнить этот массив, нужно пройтись по всем возможным итоговым счетам и типам игровых действий. При этом каждая ячейка массива A[i][j] вычисляется как сумма количества способов набрать счет j без использования текущего типа действия и количества способов набрать счет j – W[i] с учетом текущего действия.
Можно заметить, что заполнение каждой строки массива A[i] можно сделать более эффективно, если учесть уже посчитанные значения из предыдущих строк. Таким образом, для каждого нового типа действия не придется пересчитывать все с нуля, — нужно только добавлять новые комбинации. Это подход имеет временную сложность O(sn) и пространственную сложность O(sn), где s — итоговый счет, а n — количество типов игровых действий:
def num_comb_for_final_score(final_score, possible_scores):
num_comb_for_score = [1] + [0] * final_score
for play in possible_scores:
for score in range(play, final_score + 1):
num_comb_for_score[score] += num_comb_for_score[score - play]
return num_comb_for_score[-1]
final_score = 12
possible_scores = [2, 3, 7]
result = num_comb_for_final_score(final_score, possible_scores)
print(f"Количество комбинаций для достижения счeта {final_score}: {result}")
Результат:
Количество комбинаций для достижения счeта 12: 4
Задача 2: Количество маршрутов в массиве
Напишите программу для подсчета возможных способов добраться от верхнего левого угла двумерного массива до нижнего правого угла. Допустимые ходы — только вправо или вниз. Например, для массива размером 5x5 существует 70 различных путей, на рисунке показаны три из них:
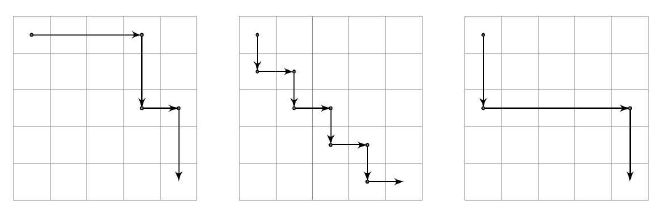
Решение
Обозначим верхний
левый угол как (0, 0). Тогда количество способов добраться до любой ячейки (i,
j) можно вычислить как сумму количества способов добраться до ячейки сверху
(i-1, j) и слева (i, j-1). Если i = 0 или j = 0, то есть если мы находимся на
границе массива, то до этой ячейки можно добраться только одним способом —
двигаясь либо только вправо, либо только вниз.
Наивное решение заключается в том, чтобы перебрать все возможные пути. Это можно сделать с помощью рекурсии, но количество путей быстро возрастает с увеличением размера массива, что делает такой подход неэффективным из-за огромной временной сложности. Оптимизировать это решение можно с помощью кэширования в матрице number_of_ways, которая в итоге будет заполнена таким образом:
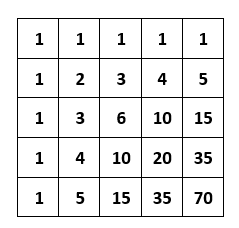
def number_of_ways(n, m):
def compute_number_of_ways_to_xy(x, y):
if x == y == 0:
return 1
if number_of_ways[x][y] == 0:
ways_top = 0 if x == 0 else compute_number_of_ways_to_xy(x - 1, y)
ways_left = 0 if y == 0 else compute_number_of_ways_to_xy(x, y - 1)
number_of_ways[x][y] = ways_top + ways_left
return number_of_ways[x][y]
number_of_ways = [[0] * m for _ in range(n)]
return compute_number_of_ways_to_xy(n - 1, m - 1)
n = m = 5
result = number_of_ways(n, m)
print(f"Количество маршрутов: {result}")
Результат:
Количество маршрутов: 70
Примечание: эту задачу также можно решить аналитически. Способ заключается в том, чтобы рассмотреть количество путей как комбинацию из n – 1 вертикальных шагов и m – 1 горизонтальных шагов. Количество возможных маршрутов можно найти с помощью биномиального коэффициента:
import math
def number_of_paths(n, m):
return math.comb(n + m - 2, m - 1)
n = m = 5
print(f"Количество маршрутов для массива {n}x{m}: {number_of_paths(n, m)}")
Результат:
Количество маршрутов для массива 5x5: 70
Задача 3: Поиск паттерна в 2D-массиве
Напишите программу, которая получает на вход матрицу (2D-массив) и паттерн (одномерный массив), и проверяет, встречается ли этот паттерн в 2D-массиве. Считается, что паттерн встречается в матрице, если входящие в паттерн числа можно обнаружить путем последовательного перемещения по соседним ячейкам (вверх, вниз, влево, вправо). К примеру, паттерн (1, 3, 4, 6) входит в показанную на рисунке матрицу, а (1, 2, 3, 4) — нет:
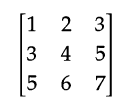
Решение
Для решения задачи нужно искать в матрице последовательности, которые соответствуют паттерну, начиная с первого элемента и проверяя все ячейки матрицы по очереди. Если первый элемент паттерна совпадает с элементом в матрице, проверяем, можем ли мы найти оставшуюся часть паттерна, перемещаясь по соседним ячейкам. Это можно сделать с помощью рекурсивного обхода. Чтобы избежать повторных проверок тех же участков, используем кэширование. Сложность этого решения равна O(nm|d|), где d — длина паттерна.
def is_pattern_in_matrix(matrix, pattern):
def search_pattern(x, y, offset):
if len(pattern) == offset:
return True
if (0 <= x < len(matrix) and 0 <= y < len(matrix[x]) and
matrix[x][y] == pattern[offset] and (x, y, offset) not in previous_attempts and
any(search_pattern(x + a, y + b, offset + 1)
for a, b in ((-1, 0), (1, 0), (0, -1), (0, 1)))):
return True
previous_attempts.add((x, y, offset))
return False
previous_attempts = set()
return any(search_pattern(i, j, 0)
for i in range(len(matrix))
for j in range(len(matrix[i])))
matrix = [[1, 2, 3],
[3, 4, 5],
[5, 6, 7]]
pattern = [1, 3, 4, 6, 7]
print(is_pattern_in_matrix(matrix, pattern))
Результат:
True
Задача 4: Путь с наименьшим весом
Дана треугольная последовательность чисел. Требуется найти путь с минимальным весом, который начинается с вершины треугольника и спускается вниз, переходя только на соседние элементы по вертикали или диагонали, и заканчивается на нижнем ряду. Вес пути определяется как сумма элементов этого пути. На приведенном ниже рисунке путь с наименьшим весом 15 выделен красным:
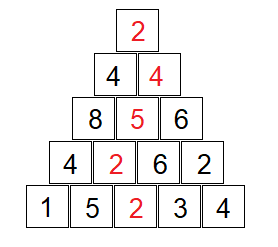
Решение
Вместо того, чтобы проверять все возможные пути (что привело бы к экспоненциальной сложности), мы будем строить решение постепенно, начиная с верхнего ряда треугольника и двигаясь вниз, вычисляя минимальный вес пути до каждой точки.
Начнем
с первой строки треугольника, где путь с минимальным весом до единственного
элемента равен значению этого элемента. Для каждой
следующей строки треугольника будем вычислять минимальный вес пути до каждого
элемента этой строки, используя минимальные веса путей до элементов предыдущей
строки. Временная сложность этого решения — O(n2), пространственная — O(n).
def minimum_path_weight(triangle):
min_weight_to_curr_row = [0]
for row in triangle:
min_weight_to_curr_row = [
row[j] +
min(
min_weight_to_curr_row[max(j - 1, 0)],
min_weight_to_curr_row[min(j, len(min_weight_to_curr_row) - 1)]
)
for j in range(len(row))
]
return min(min_weight_to_curr_row)
triangle = [[2],
[4, 4],
[8, 5, 6],
[4, 2, 6, 2],
[1, 5, 2, 3, 4]]
print(f"Путь с минимальным весом: {minimum_path_weight(triangle)}")
Результат:
Путь с минимальным весом: 15
Задача 5: Лестница
Предположим, что вы поднимаетесь по лестнице, и можете пройти за один шаг от 1 до k ступеней. Ваша цель — подняться на точно n ступеней. Напишите программу, которая принимает на вход числа n и k и возвращает количество способов, которыми можно достичь вершины. Например, если n = 4 и k = 2, то существует 5 способов подняться на вершину:
- Четыре раза по одной ступени.
- Два раза по одной ступени, затем один раз на две ступени.
- Один раз на одну ступень, затем один раз на две ступени, и снова на одну ступень.
- Один раз на две ступени, затем два раза по одной ступени.
- Два раза по две ступени.
Решение
Количество способов достичь вершины лестницы, учитывая, что каждый шаг может быть от 1 до k ступенек, можно выразить через рекурсивное уравнение:
Вернемся к приведенному выше примеру и вычислим количество способов достичь 4-й ступеньки лестницы, делая шаги длиной максимум 2.
Начнем с F(4,2): F(4,2) = F(4-2,2) + F(4-1,2) F(4,2) = F(2,2) + F(3,2). Теперь разложим F(2,2): F(2,2) = F(2-2,2) + F(2-1,2) F(2,2) = F(0,2) + F(1,2). Здесь у нас есть базовые случаи: F(0,2) = 1 (только один способ достичь нулевой ступеньки — не делать шагов) и F(1,2) = 1 (только один способ достичь первой ступеньки — сделать один шаг длиной 1).
Теперь разберем F(3,2): F(3,2) = F(3-2,2) + F(3-1,2) F(3,2) = F(1,2) + F(2,2). Мы уже знаем эти значения:
- F(1,2) = 1 (базовый случай).
- F(2,2) = 2 (вычислено ранее).
Следовательно, F(3,2) = 1 + 2 = 3. Наконец, подставляем значения обратно в F(4,2): F(4,2) = F(2,2) + F(3,2) = 2 + 3 = 5.
Таким образом, существует 5 способов достичь 4-й ступеньки лестницы.
Для улучшения пространственной сложности можно использовать массив для хранения количества способов добраться до каждой ступени, начиная с первой и до n. Каждый элемент массива будет содержать количество способов добраться до соответствующей ступени, используя результаты предыдущих вычислений. Временная сложность решения равна O(nk):
def number_of_ways_to_top(n, k):
number_of_ways_to_h = [0] * (n + 1)
number_of_ways_to_h[0] = 1
for i in range(1, n + 1):
number_of_ways_to_h[i] = sum(number_of_ways_to_h[i - j] for j in range(1, min(k, i) + 1))
return number_of_ways_to_h[n]
n = 4
k = 2
result = number_of_ways_to_top(n, k)
print(f"Количество способов достичь {n}-й ступеньки с максимальным шагом {k}: {result}")
Результат:
Количество способов достичь 4-й ступеньки с максимальным шагом 2: 5
Задача 6: Самая длинная неубывающая подпоследовательность
Проблема нахождения самой длинной неубывающей подпоследовательности в последовательности целых чисел встречается во многих сферах, от анализа текста до логики карточных игр. Например, для массива в приведенном ниже примере длина самой длинной невозрастающей подпоследовательности равна 4, и таких последовательностей несколько: (0, 8, 12, 14); (0, 4, 6, 9); (0, 2, 10, 14) — элементы подпоследовательности необязательно должны быть расположены рядом:

Напишите программу для поиска самой длинной неубывающей подпоследовательности в полученном массиве целых чисел.
Решение
Определим массив L, где L[i] будет хранить длину самой длинной невозрастающей подпоследовательности, оканчивающейся в индексе i:
- L[0] = 1 (так как нет элементов перед элементом 0)
- L[1] = 1 + max(L[0]) = 2 (так как A[0] ≤ A[1])
- L[2] = 1 + max(L[0]) = 2 (так как A[0] ≤ A[2] и A[1] > A[2])
- L[3] = 1 + max(L[0], L[1], L[2]) = 3 (так как A[0], A[1] ≤A[3] и A[2] ≤ A[3])
- L[4] = 1 + max(L[0]) = 2 (так как A[0] ≤ A[4], A[1], A[2] и A[3] > A[4])
- L[5] = 1 + max(L[0], L[1], L[2], L[4]) = 3 (так как A[0], A[1], A[2], A[4] ≤ A[5] и A[3] > A[5])
- L[6] = 1 + max(L[0], L[2], L[4]) = 3 (так как A[0], A[2], A[4] ≤ A[6] и A[1], A[3], A[5] > A[6])
- L[7 ] = 1 + max(L[0], L[1], L[2], L[3], L[4], L[5], L[6]) = 4 (так как A[0], A[1], A[2], A[3], A[4], A[5], A[6] ≤ A[7])
- L[8] = 1 + max(L[0]) = 2 (так как A[0] ≤ A[8] и A[1], A[2], A[3], A[4], A[5], A[6], A[7] > A[8])
- L[9] = 1 + max(L[0], L[1], L[2], L[4], L[6], L[8]) = 4 (так как A[0], A[1], A[2], A[4], A[6], A[8] ≤ A[9])
Временная сложность решения — O(n2):
def max_nondecreasing_sub(A):
max_length = [1] * len(A)
for i in range(1, len(A)):
max_length[i] = max(1 + max(
[max_length[j] for j in range(i)
if A[i] >= A[j]], default=0), max_length[i])
return max(max_length)
A = [0, 8, 4, 12, 2, 10, 6, 14, 1, 9]
print(f"Наибольшая длина неубывающей подпоследовательности равна {max_nondecreasing_sub(A)}")
Результат:
Наибольшая длина неубывающей подпоследовательности равна 4
Задача 7: Биномиальный коэффициент
Биномиальный коэффициент определяет количество способов выбрать k-элементное подмножество из n-элементного множества:
Основная проблема заключается в том, что если считать это число напрямую, можно столкнуться с переполнением — когда промежуточные вычисления становятся слишком большими для хранения в типичных переменных. Например, даже если итоговое значение поместится в память компьютера, промежуточные результаты могут превысить допустимый диапазон.
Нужно создать такой алгоритм, который при вычислении биномиального коэффициента не будет переполнять память, если окончательное значение вписывается в допустимые размеры переменных, например, 32-битное целое число.
Решение
Биномиальный коэффициент можно вычислить по формуле:
Рассмотрим пример вычисления по этой формуле для (5, 3):
- Базовые случаи (n, 0) и (n, n) всегда равны 1, потому что есть только один способ не выбрать ничего или выбрать все сразу.
- (5, 3) = (4, 2) + (4, 3)
- (4, 2) = (3, 1) + (3, 2)
- (4, 3) = (3, 2) + (3, 3)
- (3, 1) = (2, 0) + (2, 1) = 1 + 2 = 3
- (3, 2) = (2, 1) + (2, 2) = 2 + 1 = 3
- (4, 2) = 3 + 3 = 6
- (4, 3) = 3 + 1 = 4
- (5, 3) = 6 + 4 = 10
Для улучшения временной сложности до O(nk) необходимо использовать мемоизацию (кэширование промежуточных результатов):
def binomial_coefficient(n, k):
def compute_x_choose_y(x, y):
if y in (0, x):
return 1
if x_choose_y[x][y] == 0:
without_y = compute_x_choose_y(x - 1, y)
with_y = compute_x_choose_y(x - 1, y - 1)
x_choose_y[x][y] = without_y + with_y
return x_choose_y[x][y]
x_choose_y = [[0] * (k + 1) for _ in range(n + 1)]
return compute_x_choose_y(n, k)
n = 5
k = 3
print(binomial_coefficient(n, k))
Результат:
10
Заключение
Динамическое программирование требует глубокого понимания структуры задачи и умения выявлять повторяющиеся подзадачи. Процесс разработки алгоритма с использованием ДП обычно включает несколько важных шагов:
- Необходимо определить структуру оптимального решения подзадачи.
- Затем следует сформулировать рекуррентное соотношение, связывающее решения подзадач с решением исходной задачи.
- После этого важно выбрать правильную стратегию реализации — от простой рекурсии с мемоизацией до более эффективного итеративного подхода с табличным заполнением.
Также важно помнить, что несмотря на свою мощь, ДП не является универсальным решением: его эффективность зависит от конкретной задачи и может варьироваться от случая к случаю. В некоторых ситуациях применение ДП может привести к избыточному использованию памяти или усложнению кода без значительного выигрыша в производительности.


Комментарии