Практическое введение в динамическое программирование в картинках для непонимающих. Пошаговый разбор решения трех реальных задач.
Динамическое программирование (dynamic programming, DP) – это особый подход к решению сложных рекурсивных задач, состоящих из повторяющихся подзадач. "Наивные" методы решения предполагают многократное выполнение одних и тех же действий, что приводит к неэффективному расходованию ресурсов. DP успешно борется с этой проблемой.
В сети вы можете найти массу материалов на эту тему. Среди них очень много хороших, но очень мало наглядных. Поэтому специально для визуалов и любителей рассматривать картинки мы подготовили руководство с большим количеством иллюстраций.
Динамическое программирование и числа Фибоначчи
Классическая проблема, которая демонстрирует мощь динамического программирования, – вычисление чисел Фибоначчи. Если вы вдруг подзабыли, последовательность Фибоначчи начинается с двух единиц, а каждый следующий элемент равен сумме двух предыдущих:
1, 1, 2, 3, 5, 8, 13, 21, …
Каноническая формула для вычисления n-ного элемента ряда выглядит так:
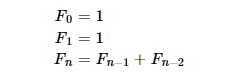
Переведем эти формулы в код, используя язык программирования Python:
def fib(n):
# можно еще добавить проверку на отрицательное число и выбрасывать ошибку
if n == 0: return 1
if n == 1: return 1
return fib(n - 1) + fib(n - 2)
Алгоритм очень прост, но есть одна проблема. Чем больше n, тем медленнее работает функция. Запустим ее 100 раз с разными входными данными (n = 10, 20 и 30) и измерим время выполнения:
>>> import timeit
>>> timeit.timeit('fib(10)', number=100, globals=globals())
0.01230633503291756
>>> timeit.timeit('fib(20)', number=100, globals=globals())
0.3506886550458148
>>> timeit.timeit('fib(30)', number=100, globals=globals())
34.2489672530209
Ничего себе! Увеличение n с 10 до 20 привело к увеличению времени в 30 раз, а с 20 до 30 – аж в 100 раз! Чтобы понять, почему так происходит, взглянем на дерево вызовов.
Предположим, необходимо вычислить F5. Решение этой задачи базируется на нескольких подзадачах:
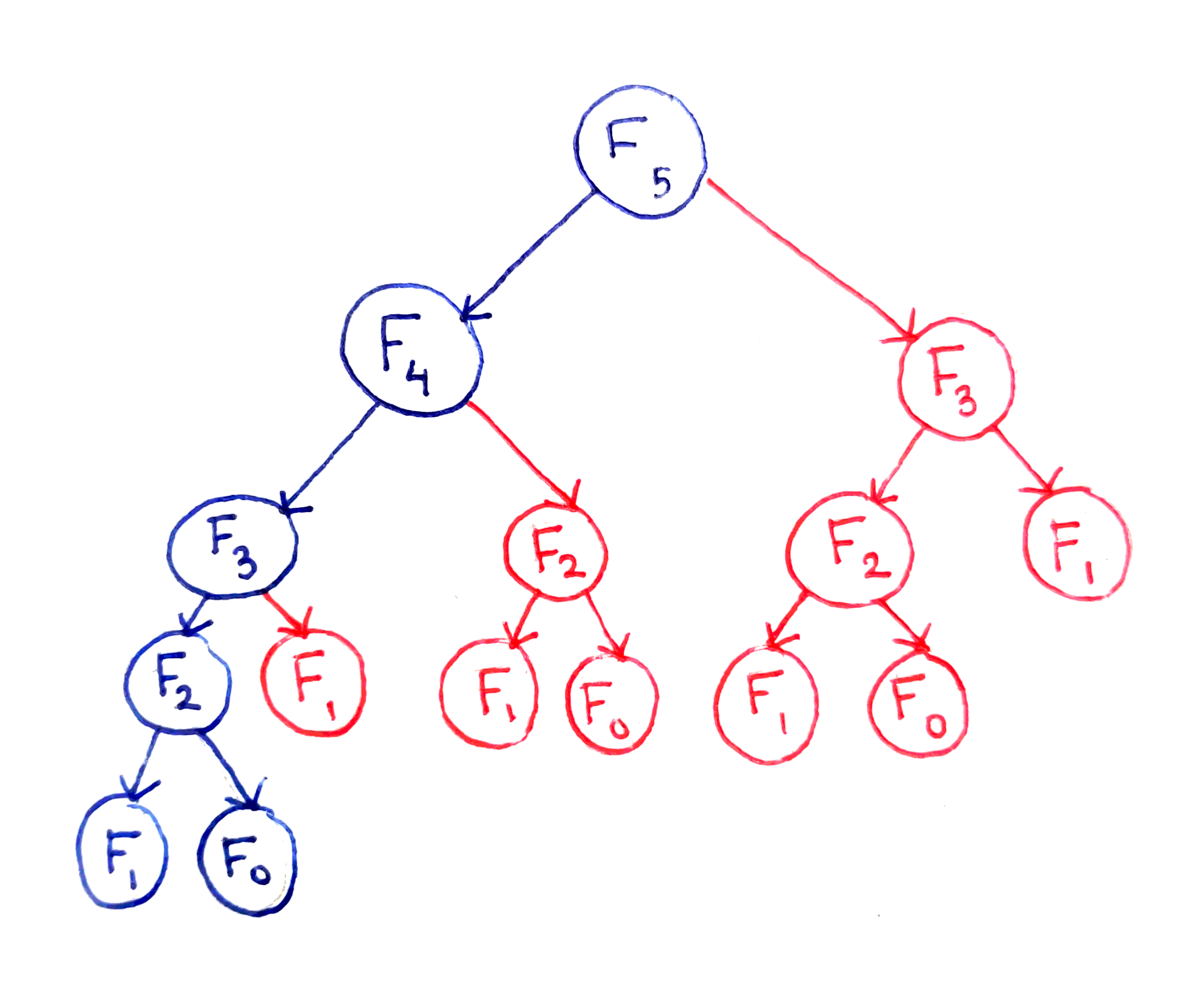
Фундаментальная проблема заключается в многократном выполнении одинаковых вычислений. Например, F3 рассчитывается дважды, а F2 – трижды, хотя результат каждый раз получается одинаковый. Даже если не углубляться в анализ времени выполнения, очевидно, что для этого алгоритма оно будет расти по экспоненте.
На решении подобных проблем и специализируется динамическое программирование. Оно помогает решать рекурсивные задачи с сильно перекрывающейся структурой подзадач. Это означает, что некоторые действия повторяются снова и снова, с одинаковыми входными данными и результатом.
Не каждая задача пригодна для DP. Если подпроблемы не перекрываются, следует использовать алгоритм "разделяй и властвуй", как при сортировке массива слиянием.
Мемоизация
Один из способов избежать постоянного пересчитывания одних и тех же данных – кешировать результаты вычислений. Технически это реализуется так:
- Если кеш содержит результат для полученных входных данных, использовать значение из кеша.
- В противном случае, вычислить результат и сохранить его в кеше, поставив в соответствие с входными данными.
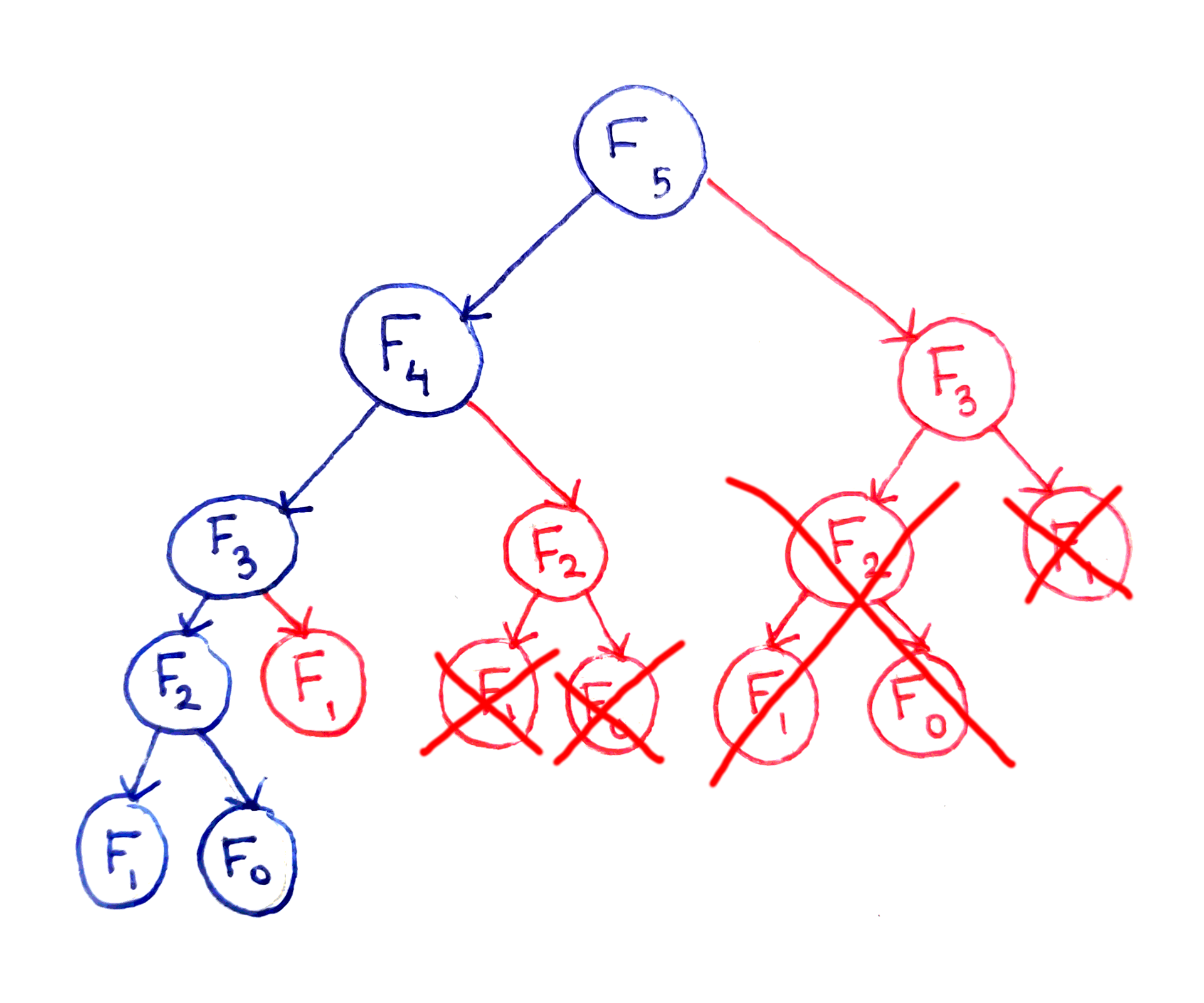
Преобразуем простой рекурсивный алгоритм в кэширующий:
def fib(n, cache=None):
if n == 0: return 1
if n == 1: return 1
if cache is None: cache = {}
if n in cache: return cache[n]
result = fib(n - 1, cache) + fib(n - 2, cache)
cache[n] = result
return result
И снова измерим его скорость:
>>> timeit.timeit('fib(10)', number=100, globals=globals())
0.0023695769486948848
>>> timeit.timeit('fib(20)', number=100, globals=globals())
0.0049970539985224605
>>> timeit.timeit('fib(30)', number=100, globals=globals())
0.013770257937721908
Зависимость от n практически линейна!
Но что насчет пространственной сложности? Для вычисления Fn нужно вычислить Fn-1 и Fn-2, и так далее до F0. Следовательно, придется кэшировать O(n) результатов. Значит, потребуется O(n) памяти.
Можно ли сделать лучше? В этом случае можно!
Динамическое программирование снизу вверх
Простая мемоизация результатов, с которой мы только что имели дело – это классический подход сверху вниз. Но можно коварно зайти и с другой стороны.
Взгляните на эту диаграмму, где каждая подзадача показана только один раз. Это цепочка зависимостей задач. Если две разные проблемы зависят (базируются) от одной и той же подпроблемы, то на нее будут указывать две стрелки.
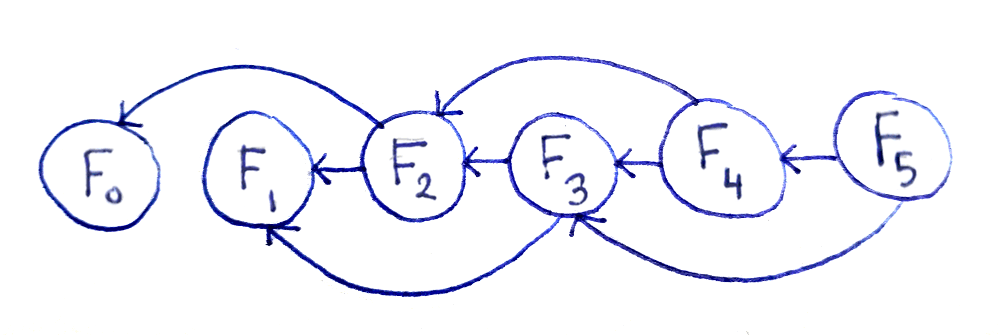
Такая точка зрения позволяет сделать сразу несколько важных заключений. Прежде всего, у нас есть O(n) подпроблем. Кроме того, эта диаграмма является направленным ациклическим графом (DAG), что означает:
- есть узлы (задачи) и ребра (зависимости между ними);
- ребра имеют направление, одна подзадача зависит от другой;
- нет циклов, значит нельзя начать с одной подзадачи и, следуя по стрелкам, вернуться к ней же.
В направленном ациклическом графе можно упорядочить вершины таким образом, что если пройти через них по очереди, вы будете всегда следовать направлению стрелок. Практически это означает, что можно расставить подзадачи таким образом, чтобы всегда иметь нужный результат еще до того, как он понадобится в более крупной задаче.
Для ряда Фибоначчи этот порядок соответствует увеличению входных данных. То есть сначала мы должны вычислить F0, затем F1, F2 и так далее до Fn.
Есть еще одна важная вещь, которую мы можем вывести из DAG. Каждая подзадача зависит только от двух других. Если вы вычисляете Fm, то вам нужны только результаты Fm-1 и Fm-2, и совершенно не нужно Fm-10. То есть вы можете спокойно выбрасывать значения, которые не участвуют в текущем вычислении.
Формализация алгоритма
- Заведем две локальные переменные, которые будут представлять последние два числа Фибоначчи, с которыми мы работаем.
- Поместим в них F0(=1) и F1(=1)
- Изменяя i от 2 до n вычислим Fi. Каждая операция зависит только от Fi-1 и Fi-2, которые хранятся в локальных переменных. Получая результат, мы выбрасываем Fi-2, заменяем его на Fi-1, а в оставшуюся переменную записываем Fi.
В Python это выглядит так:
def fib(n):
a = 1 # f(i - 2)
b = 1 # f(i - 1)
for i in range(2, n + 1):
a, b = b, a + b
return b
Зависимость времени выполнения этого алгоритма от входных данных тоже линейная (вы можете запустить его и проверить). Кроме того мы здорово сократили пространственную сложность до константного значения, храня всего лишь два предыдущих результата. Это очень круто!
Этот подход называется "снизу-вверх" (bottom-up approach), так как основывается на решении небольших подзадач с целью построения более крупных.
Динамическое программирование и задача о воришке
Теперь мы можем испытать динамическое программирование в решении более сложных проблем. Возьмем, например, задачу о воре (The House Robber Problem), который собирается ограбить целый квартал домов. В каждом i-том доме есть чем поживиться (ценность имущества - vi). Однако системы безопасности домов связаны между собой, и если вор попытается ограбить соседние дома, сработает сигнализация.
Вопрос в том, как много он сможет украсть?
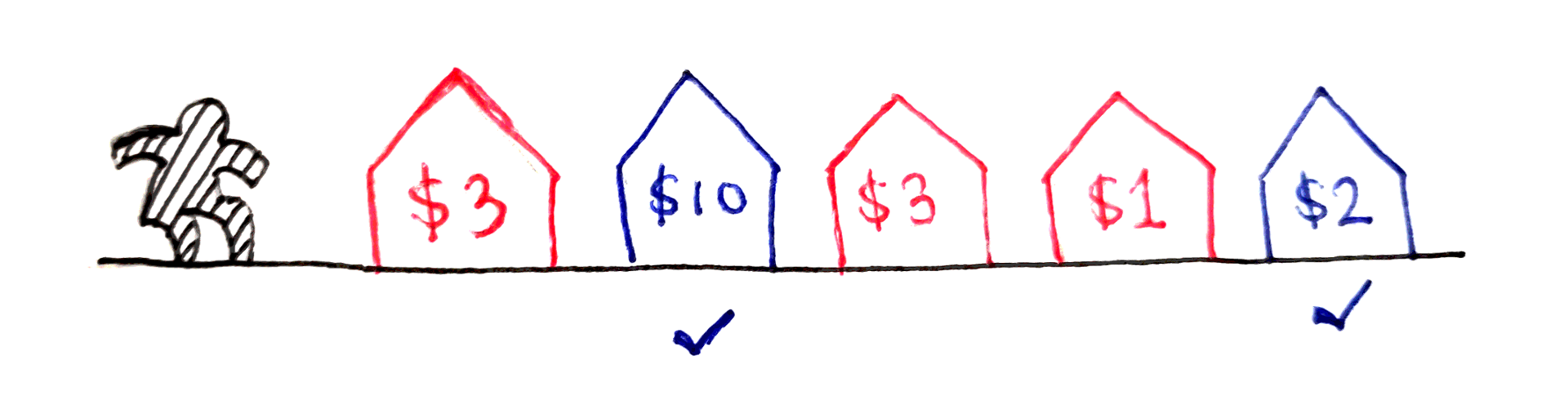
В примере, изображенном на картинке, ценность имущества в каждом доме равна соответственно 3, 10, 3, 1 и 2. Максимальная выгода – 12 – получается при ограблении второго и пятого домов.
Определение подзадач
Самый первый и важный шаг в решении любой задачи динамического программирования – определение подпроблем.
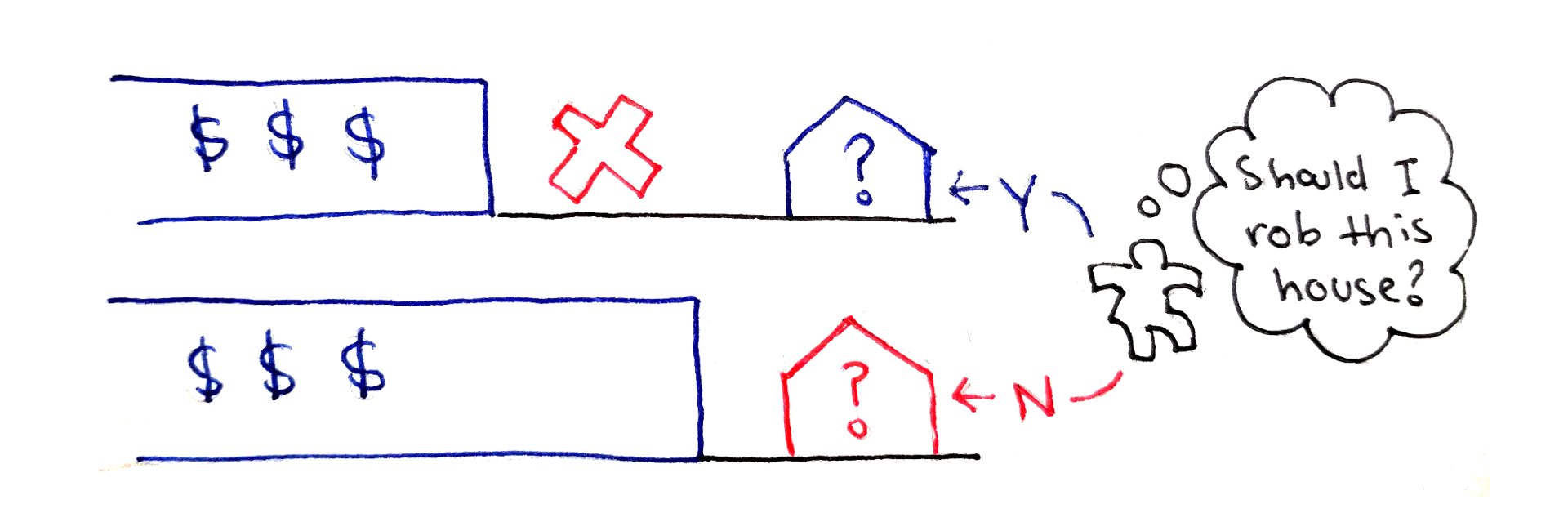
Для любого i-того дома есть две альтернативы:
- ограбить его. Но после этого увеличить выгоду вы можете только в доме
i-2, так какi-1теперь для вас закрыт. В этом случае к текущей сумме добавляется значение vi. - пропустить его. Теперь вы можете переходить к дому
i-1, он доступен для ограбления. Но к текущей сумме ничего не добавляется.
Определение рекуррентного отношения
Необходимо четко оформить вышеизложенные размышления в виде функции со следующими свойствами:
- Она должна идентифицироваться по некоторым целочисленным входным данным. Это позволит связать вход с вычисленным результатом и выполнять вычисления в определенном порядке.
- Решение должно быть легко извлекаемо, иначе функция не имеет для нас никакой пользы.
- Функция должна основываться сама на себе.
Это и есть рекуррентное отношение – выражение одних членов последовательности через другие.
Вот такую формулу мы получаем для задачи о воришке:
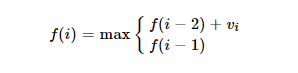
f(i) – это максимальная прибыль, которую можно получить, ограбив дома с 0 по i.
В конечно итоге мы хотим получить значение f(n-1), где n – количество домов в квартале (если индексы начинаются с 0).
Решение снизу вверх
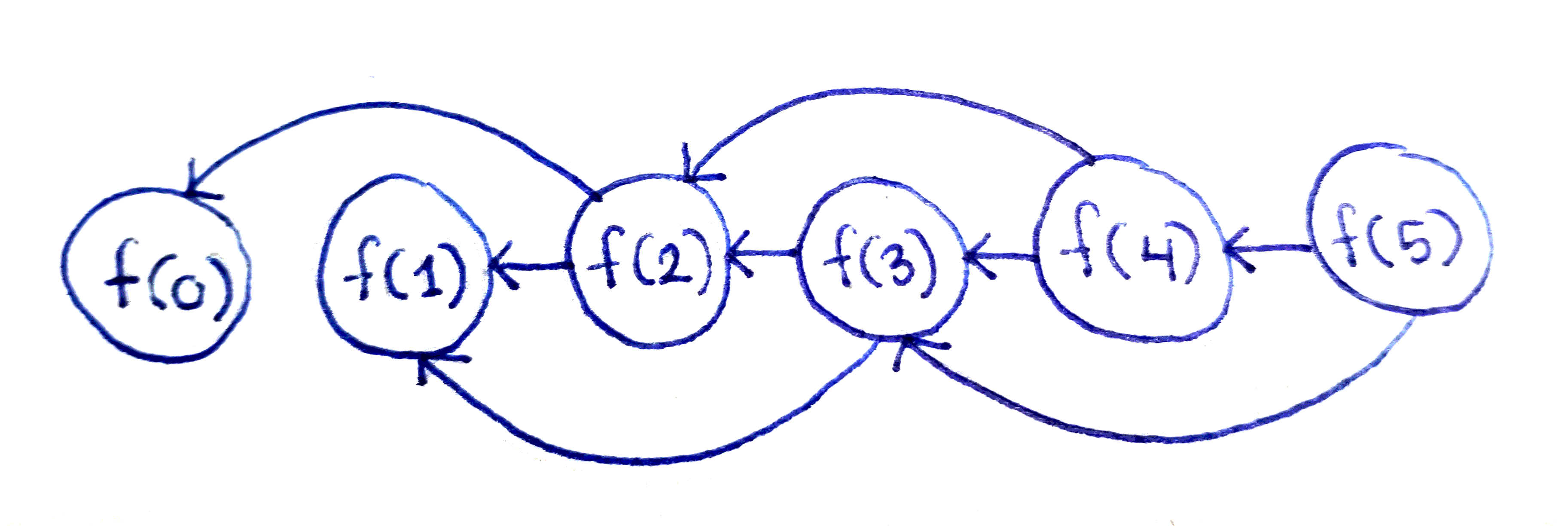
Если построить граф соотношений подзадач, то мы получим уже знакомую картинку! Каждый узел f(i) здесь зависит только от двух предыдущих: f(i-1) и f(i-2). Кроме того существует n подзадач: от f(0) до f(n-1). Следовательно мы можем решить проблему за O(n) времени, используя O(1) памяти, как уже делали это с числами Фибоначчи. Другими словами – вычисляя подзадачи в порядке увеличения индекса и сохраняя два последних результата.
def house_robber(house_values):
a = 0 # f(i - 2)
b = 0 # f(i - 1)
for val in house_values:
a, b = b, max(b, a + val)
return b
Реализация отличается только способом объединения двух значений – раньше мы их просто складывали, а теперь еще и выбираем максимум.
Динамическое программирование и задача о размене монет
Обе предыдущие задачи были одномерными, состоящими из линейной последовательности подзадач. Давайте поднимемся на уровень выше – к двумерной структуре.
По условию известной задачи о размене монет (Change-making problem) у вас есть несколько номиналов (d1, d2, …, dn) и неограниченное количество монет каждого номинала. С их помощью нужно набрать определенную сумму c. Суть задачи – использовать как можно меньше монет.
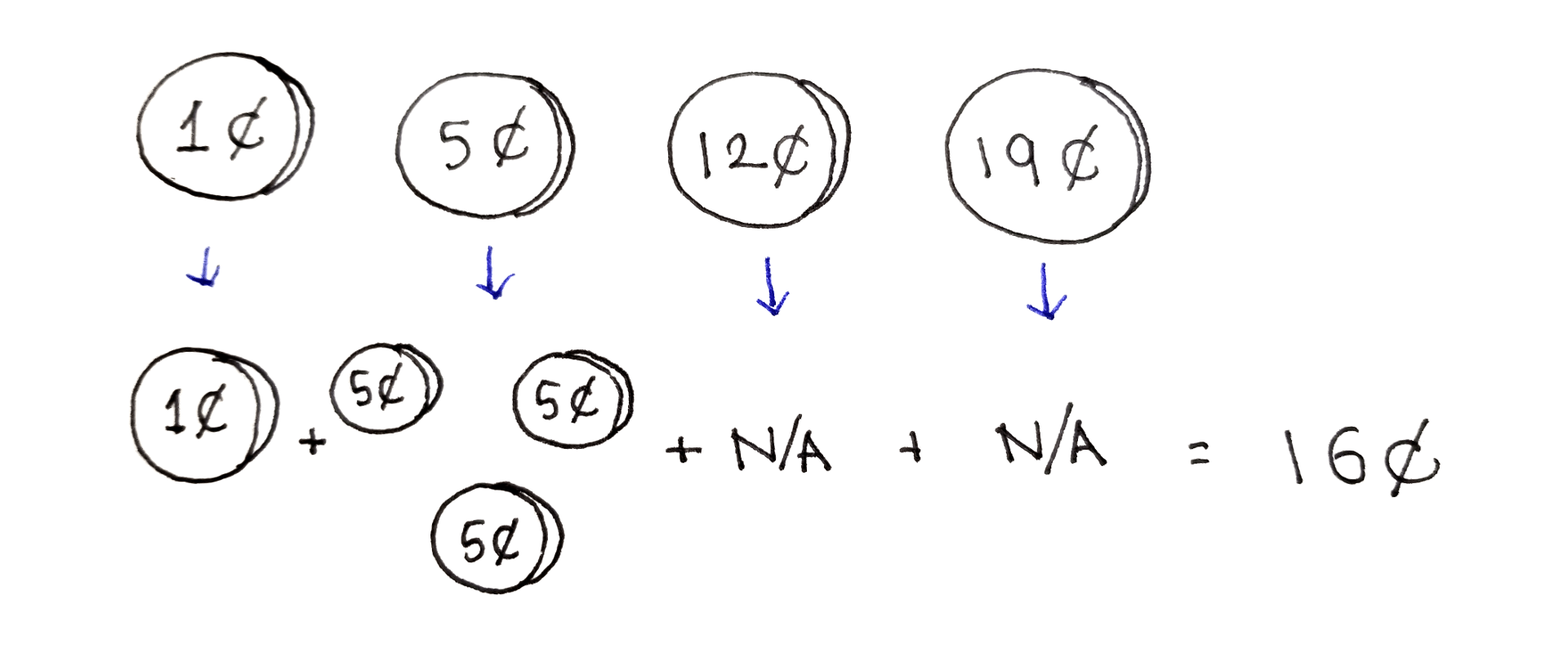
Например, у вас есть монеты номиналом 1, 5, 12, 19 центов, а набрать нужно 16 центов. Минимальное количество монет – 4: три по 5 центов и один пенни.
Обратите внимание, не всегда имеет смысл использовать самый большой из подходящих номиналов. Ведь если бы вы взяли монету в 12 центов, то пришлось бы добавить еще четыре пенни и всего вышло бы 5 монет.
Установим пару правил:
- Номиналы монет уникальны. Технически это необязательно, но так проще.
- Номиналы указаны в порядке возрастания стоимости. На практике их всегда можно отсортировать.
- Первый номинал всегда равен 1. Только в этом случае гарантирована возможность сбора любой суммы.
Определение подзадач
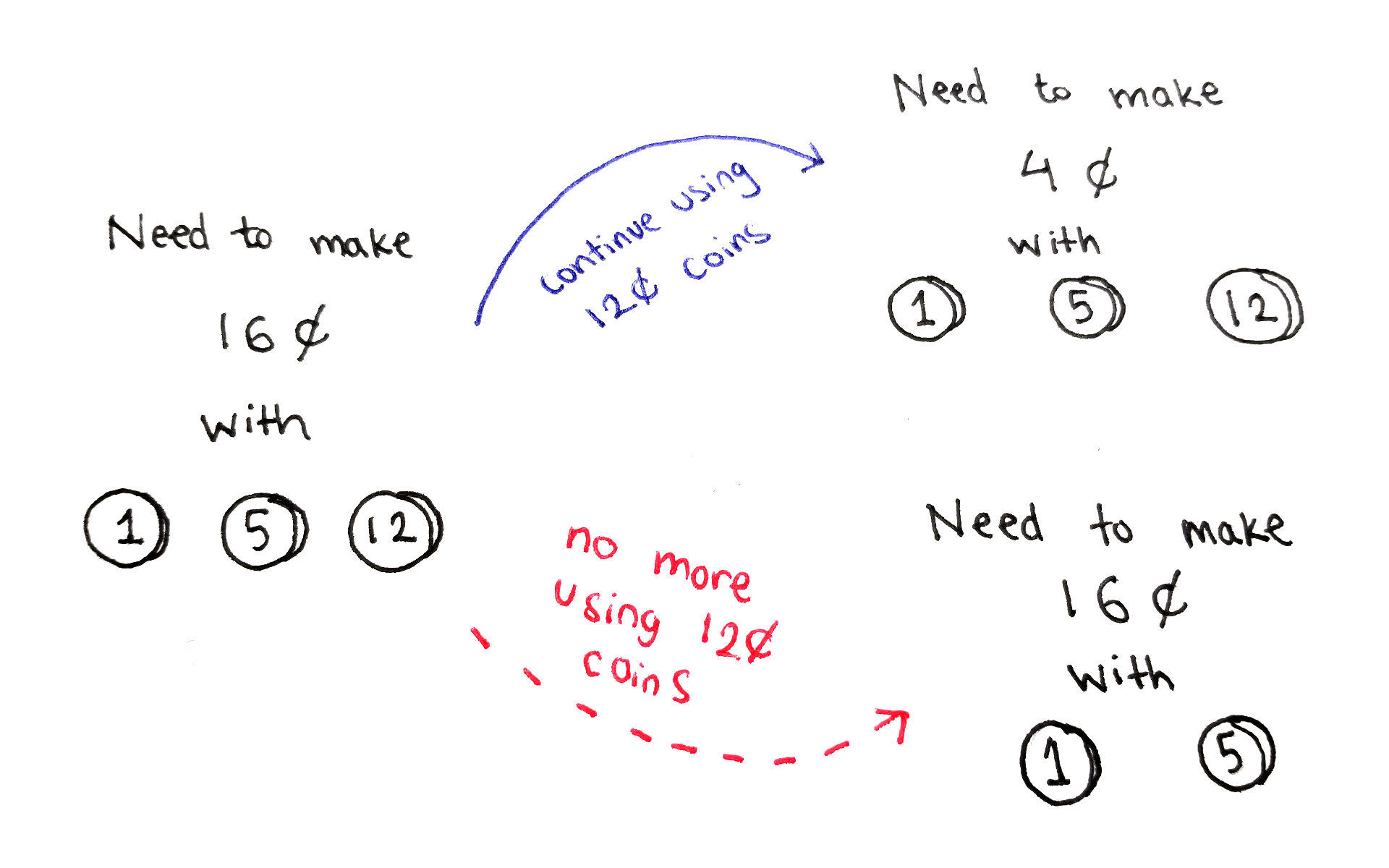
В любой момент алгоритма мы работаем с набором номиналов и целевой суммой. Есть два возможных выбора:
- Использовать монету самого большого номинала. При этом цель уменьшается, количество использованных монет увеличивается, а набор номиналов не изменяется.
- Не использовать монету самого большого номинала. При этом цель и количество монет не изменяются, а набор номиналов уменьшается.
Не в каждой ситуации возможны оба эти варианта. Например, если остался всего один номинал, то придется использовать именно его. А если достоинство монеты больше цели, придется от нее отказаться.
Определение рекуррентного отношения
Функция, которая нам нужна, будет принимать на вход два значения: подмножество номиналов, которые можно использовать, и целевую сумму, которую нужно набрать. Так как номиналы расположены в порядке убывания, достаточно иметь лишь одно целое число – индекс самого большого из них. Например, i означает, что можно использовать номиналы d0, d1, ... , di.
Теперь мы можем определить функцию f(i, t) для расчет минимального количества монет с номиналом не больше di, с помощью которых можно набрать сумму t. Вот оно – искомое рекуррентное отношение:
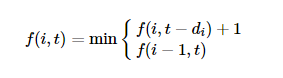
Окончательный ответ на нашу задачу соответствует f(n-1, c), где n – изначальное количество номиналов, а c – сумма, которую нужно собрать.
Граф зависимостей
Так как рекуррентное отношение имеет два целочисленных входа, подзадачи можно разложить в виде двумерной таблицы. Номиналы будут расположены по горизонтальной оси, а целевая сумма – по вертикальной.
Возьмем, например, монеты номиналом в d2=3, d1=2 и d0=1 и попробуем набрать с их помощью 5 центов. Запишем все промежуточные значения в порядке убывания снизу вверх. Текущая позиция алгоритма – в левом нижнем углу таблицы (индекс самого большого номинала – 2, сумма – 5).
Направленный граф для этой задачи довольно сложен, поэтому мы будем строить его по одному шагу за раз. Каждая ячейка индексируется двумя числами: (i, t). Здесь i – индекс номинала, а t – целевая сумма.

Из этой ячейки у нас есть два пути: либо вверх, с использованием монеты высшего достоинства, либо вправо.
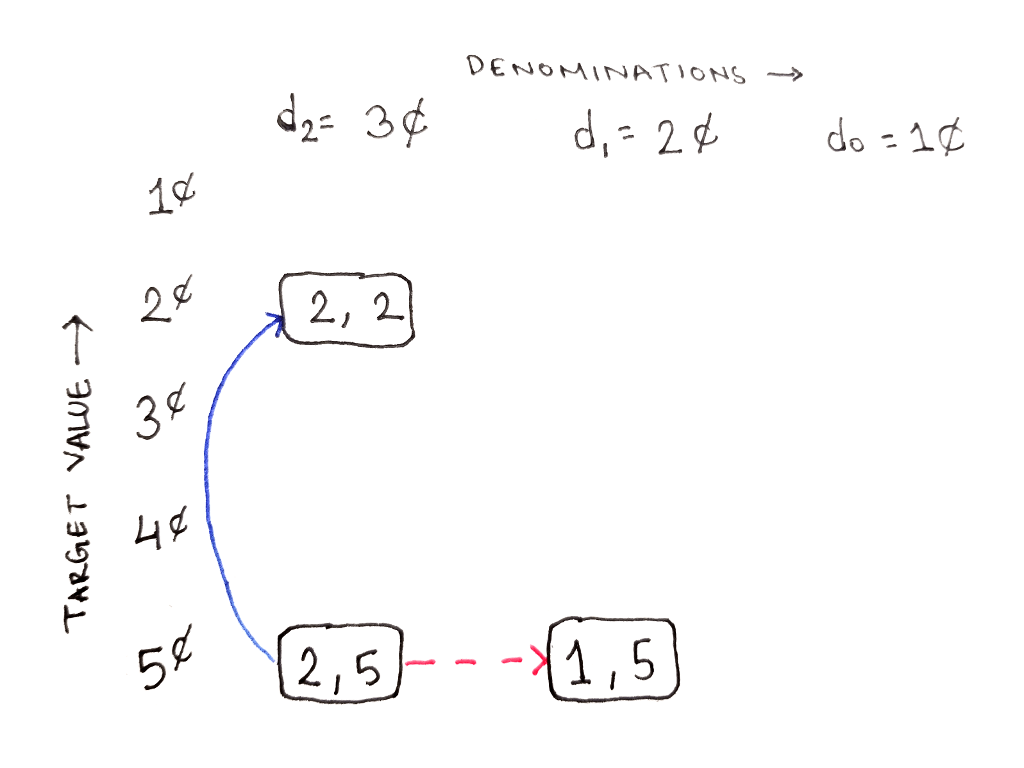
Из подзадачи (1,5) тоже есть два пути:
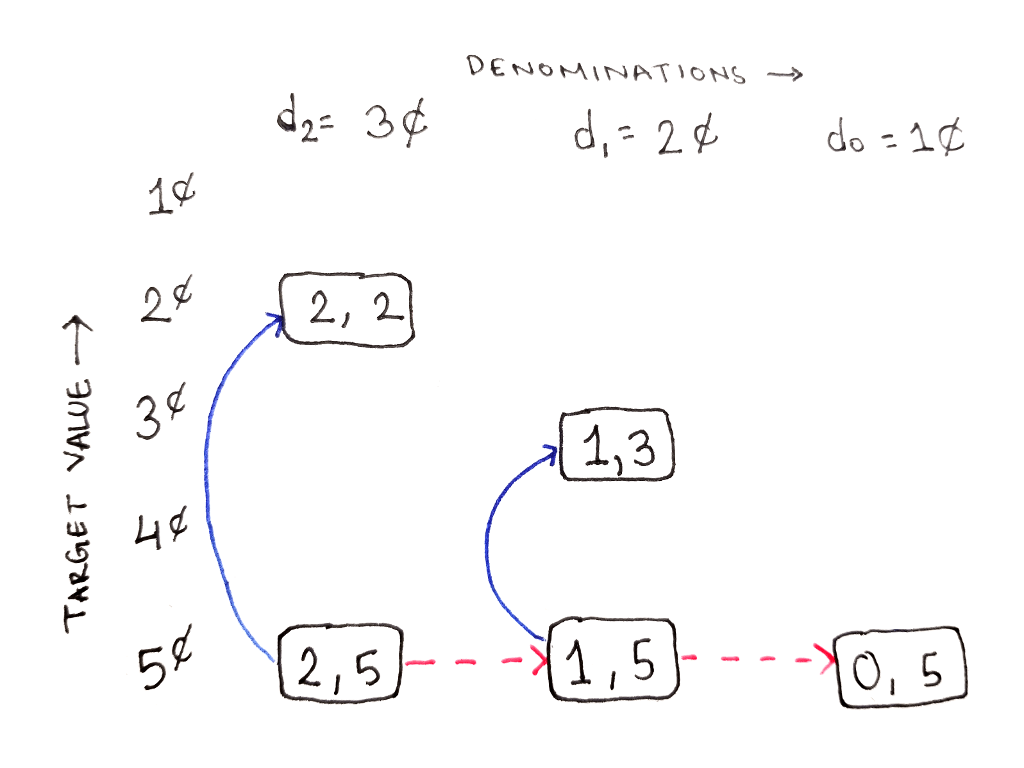
А вот из подзадачи (2,2) путь всего один, так как мы физически не можем использовать наивысший номинал в 3 цента – он больше целевой суммы (2 цента). Отсюда можно двигаться только вправо:
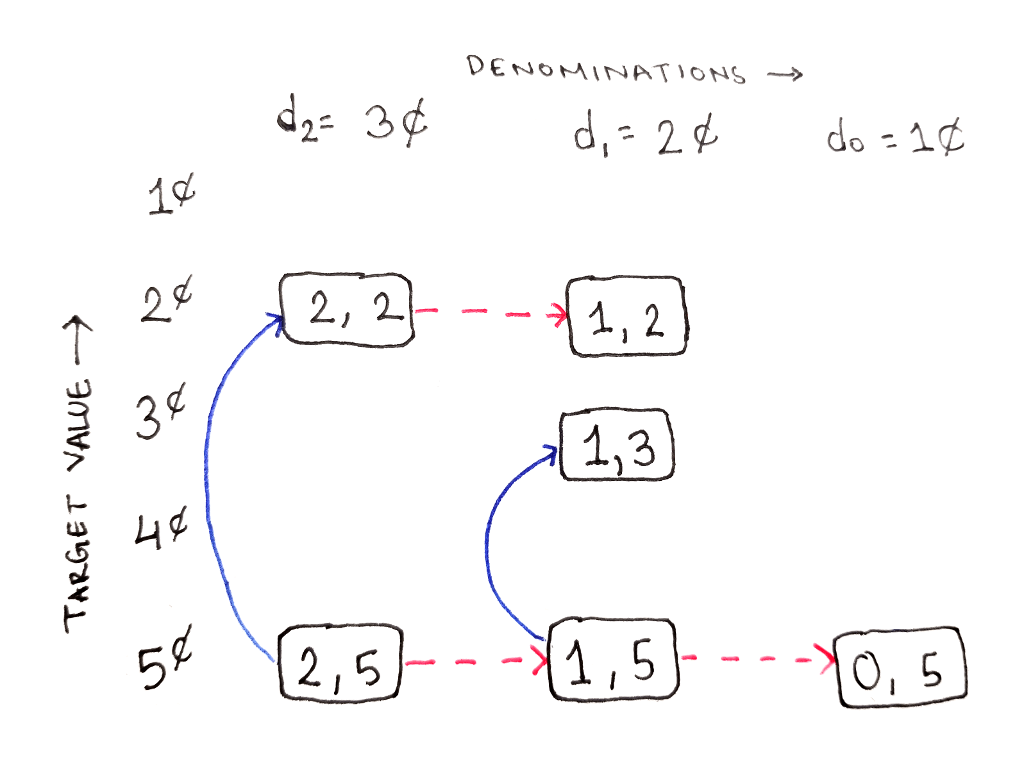
Подзадача (0, 5) тоже базируется только на одной задаче (0,4), так как остался всего один номинал. Фактически, теперь мы можем только подниматься по крайнему правому столбцу.
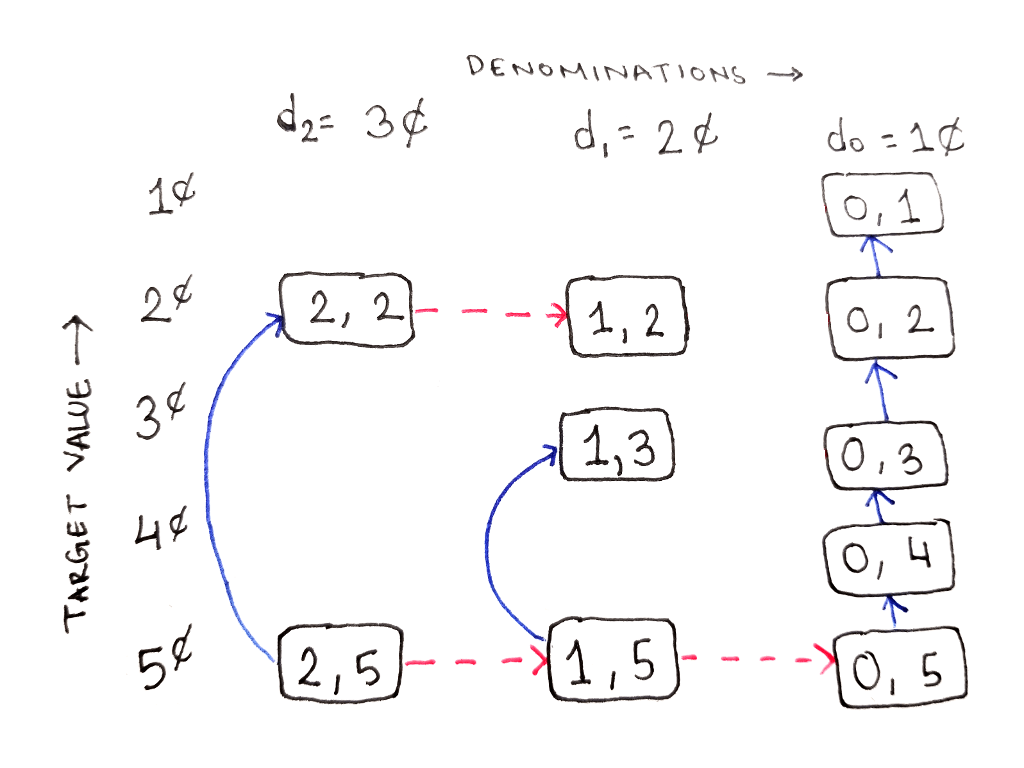
Если заполнить табличку до конца, получим вот такую структуру. Ячейки с подзадачами, которые никогда не встречаются, затемнены.
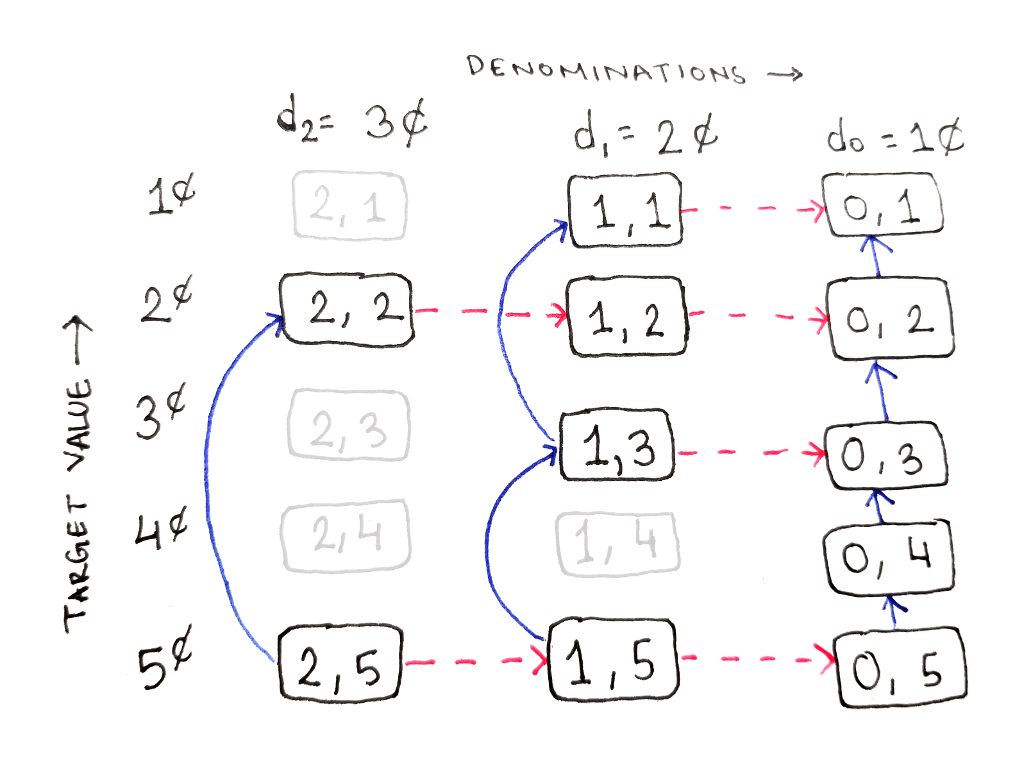
В качестве упражнения вы можете расставить стрелки зависимостей для неактивных подзадач.
Решение снизу вверх
Используем для решения задачи динамическое программирование. Из графа видно, что любая ячейка таблицы зависит только от ячеек выше нее в том же столбце и от ячеек в столбце справа. Это значит, что мы можем решать подзадачи в следующем порядке:
- Вычислить значения в одной колонке за раз, начиная с самой правой.
- В пределах столбца двигаться снизу вверх.
- При переходе к следующему столбцу сохранять только значения из предыдущего.
Конечно, не все значения в колонке нужны, однако, определить, какие можно отбросить, очень непросто. Поэтому, чтобы избежать ненужных вычислений, мы откажемся от bottom-up алгоритма и применим простую мемоизацию.
Решение с мемоизацией
По сути это дословный перевод разобранного выше рекуррентного отношения. Самое сложное тут определить , когда нельзя сделать выбор. Если ветка недоступна, мы дадим ей значение math.inf, в это случае метод min() выберет другой путь.
import math
def coins(denominations, target):
cache = {}
def subproblem(i, t):
if (i, t) in cache: return cache[(i, t)] # мемоизация
# Использование текущего номинала
val = denominations[i]
if val > t: choice_take = math.inf # текущий номинал слишком велик
elif val == t: choice_take = 1 # цель достигнута
else: choice_take = 1 + subproblem(i, t - val) # взять монету и продолжить рекурсию
# Переход к меньшему номиналу
choice_leave = (
math.inf if i == 0 # нет меньшего номинала
else subproblem(i - 1, t)) # рекурсия с имеющимся номиналом
optimal = min(choice_take, choice_leave)
cache[(i, t)] = optimal
return optimal
return subproblem(len(denominations) - 1, target)
Несмотря на использование мемоизации для уменьшения количества вычислений, оно все еще ограничено общим числом подзадач в графике. Таким образом, и время выполнения, и пространственная сложность этого алгоритма равна O(nc), где n – количество номиналов, а c – целевая сумма.
Динамическое программирование
Вот мы и познакомились с полезным методом решения рекурсивных задач с сильно перекрывающейся структурой подзадач. Его алгоритмы состоят из следующих действий:
- Определение подзадач. Обычно на каждом шаге есть выбор между двумя меньшими подзадачами.
- Составление рекуррентного отношения.
- Определение порядка выполнения подзадач. Часто бывает полезно нарисовать одномерный или двумерный график зависимостей.
- Реализация рекуррентного отношения, решение подзадач по порядку с сохранением только нужных результатов и использованием мемоизации.
Мы разобрали, как работает динамическое программирование, на примере трех известных проблем, однако оно полезно во множестве случаев. Поэтому практикуйтесь! Остались вопросы? Задайте их в комментариях!



Комментарии