🤔 Инварианты: проектирование эффективных алгоритмов

Что такое инварианты в программировании

Инварианты – это условия, которые остаются неизменными на протяжении всего выполнения программы. Такими условиями могут быть значения переменных или определенная логика выполнения алгоритма. Инварианты играют ключевую роль в проектировании эффективных алгоритмов, поскольку:

• Помогают быстро отсеять субоптимальные решения.
• Позволяют избежать лишних проверок или вычислений.
• Служат доказательством корректной работы программы.
• Упрощают реализацию итеративных решений.
• Предоставляют ключевые характеристики временной и пространственной сложности алгоритма.
  

Примеры инвариантов

Бинарный поиск

Инвариант: пространство возможных решений всегда содержит искомый элемент — на каждом шаге алгоритма мы можем быть уверены, что этот элемент находится в текущем интервале поиска.

Алгоритм быстрой сортировки

Инвариант: после каждого шага разделения, элемент-разделитель неизменно оказывается на позиции, при которой все элементы слева от него меньше или равны ему, а все элементы справа — больше. Этот инвариант:

• Помогает алгоритму эффективно сортировать массив, гарантируя, что каждый шаг приближает нас к полностью отсортированному состоянию.
• Позволяет оценить, что в среднем алгоритм будет разделять массив пополам на каждом уровне рекурсии. Это приводит к логарифмическому числу уровней рекурсии и обосновывает среднюю временную сложность O(n log n).
  

Сортировка выбором

Сортировка выбором основана на поиске наименьшего элемента, следующего наименьшего элемента и т.д., и перемещении их на соответствующие места в массиве.

Инвариант: подмассив от начала до текущей позиции всегда отсортирован, и все его элементы меньше или равны оставшимся элементам.

Более сложный пример — генерация чисел вида a + b√2

Предположим, нужно сгенерировать первые k чисел вида a + b√2, где a и b — неотрицательные целые числа, в порядке возрастания. В этом алгоритме несколько инвариантов:

• Красно-черное дерево RBTree автоматически поддерживает элементы в отсортированном порядке. Каждый раз, когда элемент добавляется или удаляется из дерева, оно перестраивается таким образом, чтобы элементы оставались отсортированными.
• В очереди никогда нет дубликатов (элемент с уже существующим ключом не будет добавлен в дерево, чтобы не обрабатывать одно и то же число несколько раз).
  
• Имеется ограничение на расстояние между элементами (новые элементы, добавляемые в очередь, имеют значения, которые являются производными от текущего наименьшего элемента).
  

        import math
from bintrees import RBTree

class ABSqrt2:
    def __init__(self, a, b):
        self.a, self.b = a, b
        self.val = a + b * math.sqrt(2)
    
    def __lt__(self, other):
        return self.val < other.val
    
    def __eq__(self, other):
        return self.val == other.val

def generate_first_k_a_b_sqrt2(k):
    candidates = RBTree([(ABSqrt2(0, 0), None)])
    result = []
    
    while len(result) < k:
        next_smallest = candidates.pop_min()[0]
        result.append(next_smallest.val)
        candidates[ABSqrt2(next_smallest.a + 1, next_smallest.b)] = None
        candidates[ABSqrt2(next_smallest.a, next_smallest.b + 1)] = None
    
    return result

k = 10
result = generate_first_k_a_b_sqrt2(k)
print(f"Первые {k} чисел вида a + b√2:")
for i, val in enumerate(result, 1):
    print(f"{i}: {val}")


    

Вывод

        Первые 10 чисел вида a + b√2:
1: 0.0
2: 1.0
3: 1.4142135623730951
4: 2.0
5: 2.414213562373095
6: 2.8284271247461903
7: 3.0
8: 3.414213562373095
9: 3.8284271247461903
10: 4.0
    

Курс «Алгоритмы и структуры данных» от proglib.academy

Алгоритмы и структуры данных – фундаментальные концепции в программировании. Их понимание критически важно для:

1. Оптимизации кода и повышения производительности программ
2. Решения сложных задач эффективным способом
   
3. Успешного прохождения технических собеседований
   

Ключевые темы для изучения:

• Базовые структуры данных (массивы, связные списки, стеки, очереди)
• Деревья и графы
  
• Алгоритмы сортировки и поиска
  
• Жадные алгоритмы
  

Освоение этих тем поможет вам:

• Писать более эффективный и оптимизированный код
• Лучше понимать работу существующих библиотек и фреймворков
  
• Развить алгоритмическое мышление
  

Независимо от выбранного пути обучения, инвестиции в знания алгоритмов и структур данных всегда окупаются в долгосрочной перспективе для любого разработчика.

Как выбрать инвариант

Выбор правильного инварианта — своего рода искусство. Два главных подхода:

• Анализ работы алгоритма на небольших наборах данных. Так можно заметить закономерности и сформулировать гипотезу об инварианте.
• Часто инвариантом может служить подмножество входных данных.
  

Рассмотрим процесс определения инварианта на примерах двух связанных между собой задач.

Задача 1: Сумма двух чисел в массиве

Нужно написать программу, которая получает отсортированный массив и число t, а затем определяет, есть ли в массиве два числа, сумма которых равна t.

Пример

В массиве [-2, 1, 2, 4, 7, 11]:

• Есть числа, дающие в сумме 6 (2 + 4).
• Есть числа, дающие в сумме 0 (-2 + 2).
  
• Есть числа, дающие в сумме 13 (2 + 11).
  
• Нет двух чисел, дающих в сумме 10.
  

Подходы к решению:

Брутфорсный алгоритм

Самый простой способ решения этой задачи — использовать два вложенных цикла для проверки каждой возможной пары элементов массива. Этот метод имеет временную сложность O(n²), где n — длина входного массива, так как каждый элемент сравнивается со всеми остальными. Очевидно, метод не подходит для больших массивов.

Хеш-таблица

Это более эффективный подход: мы добавляем каждый элемент массива в хеш-таблицу и затем для каждого элемента проверяем, существует ли в таблице число t – e, где t — целевое значение, а e — текущий элемент. Этот метод сокращает временную сложность до O(n), но требует дополнительного пространства O(n) для хранения хеш-таблицы.

Использование инварианта

Наиболее эффективный подход использует свойство отсортированности массива и принцип инвариантов. Идея состоит в том, чтобы поддерживать подмассив, который гарантированно содержит решение, если оно существует. Этот подмассив изначально включает весь массив и постепенно уменьшается с одной или другой стороны.

Уменьшение подмассива основывается на следующих наблюдениях:

• Если сумма крайнего левого и крайнего правого элементов меньше целевого значения, то крайний левый элемент никогда не может быть частью пары, которая дает целевое значение. Таким образом, его можно исключить из дальнейшего рассмотрения.
• Аналогично, если сумма этих элементов больше целевого значения, то крайний правый элемент также не может быть частью такой пары и его можно исключить.
  

Этот метод позволяет нам эффективно искать пару, сокращая размер подмассива на каждом шаге, что приводит к временной сложности O(n) без необходимости дополнительного пространства для хранения данных:

        def has_two_sum(arr, t):
    i, j = 0, len(arr) - 1
    while i <= j:
        if arr[i] + arr[j] == t:
            return True
        elif arr[i] + arr[j] < t:
            i += 1
        else:  
            j -= 1
    return False

arr = [-2, 1, 2, 4, 7, 11]
t = 0
print(has_two_sum(arr, t)) 
    

Вывод

        True
    

Задача 2: Сумма трех чисел в массиве

Нужно написать программу, которая получает неотсортированный массив и число t, и определяет, есть ли в массиве три числа (необязательно отдельных, они могут повторяться), сумма которых равна t.

Пример

В массиве [11, 2, 5, 7, 3]:

• Числа 3, 7 и 11 дают в сумме 21.
• Числа 5, 5 и 11 (5 можно повторить по условию) тоже дают в сумме 21.
  
• Но нет трех чисел, сумма которых равна 22.

Подходы к решению

Брутфорсный подход

Решение заключается в рассмотрении всех возможных троек элементов массива. Это можно сделать с помощью трех вложенных циклов, перебирающих все элементы массива. Время выполнения такого алгоритма составляет O(n³), где n — длина массива, а пространственная сложность — O(1).

Хэш-таблица

Улучшить время выполнения до O(n²) можно с помощью хэш-таблицы. Пусть arr — входной массив, а t — заданное число. Мы можем улучшить временную сложность до O(n²), сначала сохранив все элементы массива в хэш-таблице. Затем, перебирая пары элементов, для каждого arr[i] + arr[j] мы ищем t – (arr[i] + arr[j]) в хэш-таблице. Пространственная сложность при этом увеличивается до O(n).

Сортировка

Можно ускорить алгоритм и без использования дополнительной памяти — если применить сортировку. Затем для каждого элемента arr[i] мы будем искать индексы j и k такие, что arr[j] + arr[k] = t – arr[i]. Для этого мы перебираем значения arr[i] и выполняем бинарный поиск для arr[k]. Время выполнения этой операции составляет O(n log n).

Оптимизация с помощью инварианта

Мы можем улучшить временную сложность, начав с проверки суммы arr[0] + arr[n-1]. Если эта сумма равна t – arr[i], задача решена. В противном случае, если arr[0] + arr[n-1] < t – arr[i], мы переходим к проверке arr[1] + arr[n-1], поскольку нет смысла проверять arr[0] с другими элементами, так как arr[n-1] — самое большое значение в массиве. Аналогично, если arr[0] + arr[n-1] > t – arr[i], мы переходим к проверке arr[0] + arr[n-2]. Этот подход исключает элемент на каждом шаге, затрачивая O(1) времени на каждую итерацию, что в итоге дает временную сложность O(n). Инвариант заключается в том, что если два элемента, сумма которых равна t – arr[i], существуют, они должны находиться в текущем подмассиве:

        def has_two_sum(arr, t):
    i, j = 0, len(arr) - 1
    while i <= j:
        if arr[i] + arr[j] == t:
            return True
        elif arr[i] + arr[j] < t:
            i += 1
        else:  
            j -= 1
    return False

def has_three_sum(arr, t):
    arr.sort()
    return any(has_two_sum(arr, t  -  e) for e in arr)

arr = [11, 2, 5, 7, 3]
t = 21
print(has_three_sum(arr, t)) 
    

Вывод

        True
    

Временная сложность этого решения складывается из сортировки и прохода по массиву (O(n log n) + O(n) = O(n²)), а пространственная сложность равна O(1).

А теперь разберем несколько задач, которые эффективнее всего можно решить с помощью инвариантов.

Доминирующий элемент

В некоторых задачах необходимо выявить элементы в последовательности, которые встречаются чаще, чем все остальные. Например, нужно определить пользователей, которые используют чрезмерное количество сетевых ресурсов, или IP-адреса, откуда поступает наибольшее количество запросов по протоколу HTTP. Рассмотрим упрощенную версию этой задачи.

Условие

Дана последовательность строк, и известно, что более половины строк являются повторениями одной и той же строки (называемой доминирующим элементом). При этом позиции, на которых встречается доминирующий элемент, неизвестны. Напишите программу, которая за один проход по последовательности определяет доминирующий элемент. Например, если входная последовательность выглядит как ['b', 'a', 'c', 'a', 'a', 'b', 'a', 'a', 'c', 'a'], то доминирующим элементом является a, так как он встречается 6 раз из 10.

Решение

Брутфорсный подход заключается в использовании хэш-таблицы для учета количества повторений каждого уникального элемента. Временная сложность такого алгоритма составляет O(n), где n — количество элементов во входных данных, но пространственная сложность также составляет O(n).

Для более эффективного подсчета мы можем разделить элементы на две группы: те, которые содержат преобладающий элемент, и те, которые его не содержат. Поскольку первая группа больше второй, если мы видим два разных элемента, максимум один из них может быть доминирующим элементом. Отбрасывая оба, мы сохраняем разницу в размерах групп, поэтому доминирующий элемент оставшихся элементов не изменяется.

Алгоритм выглядит так

• Назначаем первый элемент последовательности кандидатом на доминирующий элемент и устанавливаем счетчик.
• Проходим по оставшимся элементам. Каждый раз, когда встречаем элемент, равный кандидату, увеличиваем счетчик. Если элемент отличается, уменьшаем счетчик.
  
• Если счетчик становится равным нулю, устанавливаем следующий элемент кандидатом.
  

Математическое обоснование

Пусть доминирующий элемент встречается m раз из n элементов. По определению доминирующего элемента, m/n > 1/2. Если мы отбрасываем два различных элемента, то:

• Случай 1: Ни один из удаленных элементов не является доминирующим элементом. Тогда в оставшемся массиве из n – 2 элементов будет m доминирующих элементов. Доля доминирующих элементов в оставшемся массиве: m/(n – 2). Так как m/n > 1/2, то m/(n – 2) > 1/2.
• Случай 2: Один из удаленных элементов является доминирующим элементом. Тогда в оставшемся массиве из n – 2 элементов будет m – 1 доминирующий элемент. Доля доминирующих элементов в оставшемся массиве: (m – 1)/(n – 2). Поскольку m/n > 1/2, то (m – 1)/(n – 2) > 1/2.
  

        def majority_search(input_stream):
    candidate, candidate_count = None, 0
    for it in input_stream:
        if candidate_count == 0:
            candidate, candidate_count = it, 1
        elif candidate == it:
            candidate_count += 1
        else:
            candidate_count -= 1
    return candidate
data = ['b', 'a', 'c', 'a', 'a', 'b', 'a', 'a', 'c', 'a']
result = majority_search(data)
print(f"Элемент, встречающийся наибольшее число раз: {result}")
    

Вывод

        Элемент, встречающийся наибольшее число раз: a
    

Оптимальный старт

Города расположены по круговой дороге. В каждом городе есть заправка с определенным запасом бензина. Ваш бак имеет неограниченную емкость, и вам нужно посетить все города и вернуться в исходный пункт. Суммарный запас бензина во всех городах равен количеству, необходимому для одного круга. Запас бензина в городе считается достаточным, если, начав с пустым баком в этом городе, можно проехать через все остальные города, заправляясь в каждом, и вернуться обратно, не израсходовав весь бензин до достижения цели. Нужно написать программу, которая определит, в каком городе запас бензина достаточен для старта успешного путешествия. Для примера на картинке городом с таким достаточным запасом является D, как мы убедимся позже:

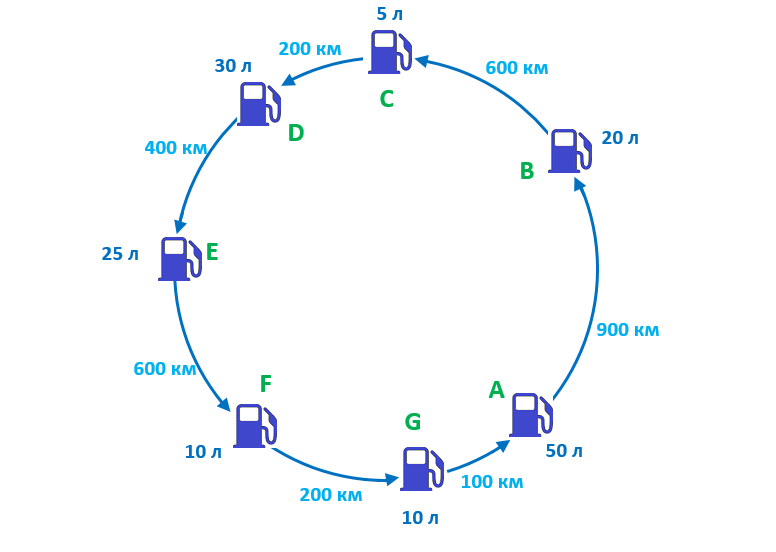
Подходы к решению

• Брутфорсный подход требует перебора всех вариантов и имеет временную сложность O(n²).
• Жадный алгоритм (выбор города с наибольшим запасом бензина или определение городов с наилучшим соотношением бензин/дистанция) не подходит. В примере на изображении город A имеет наибольший запас топлива, но если начать маршрут с A, попасть в C не получится. Ближе всего к A находится G, и у этого города самое выгодное соотношении дистанции и бензина, но если начать с него, доехать до D невозможно.

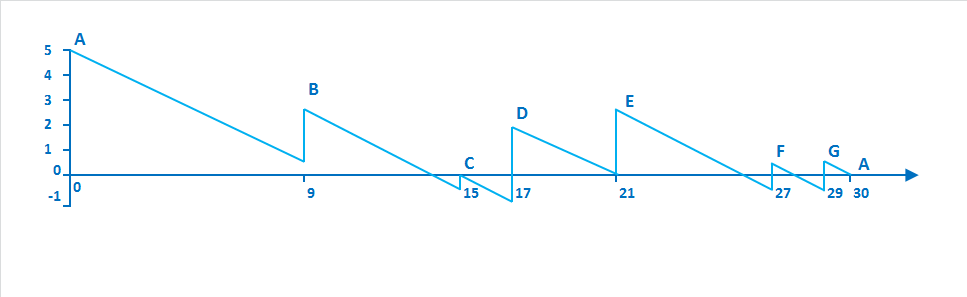
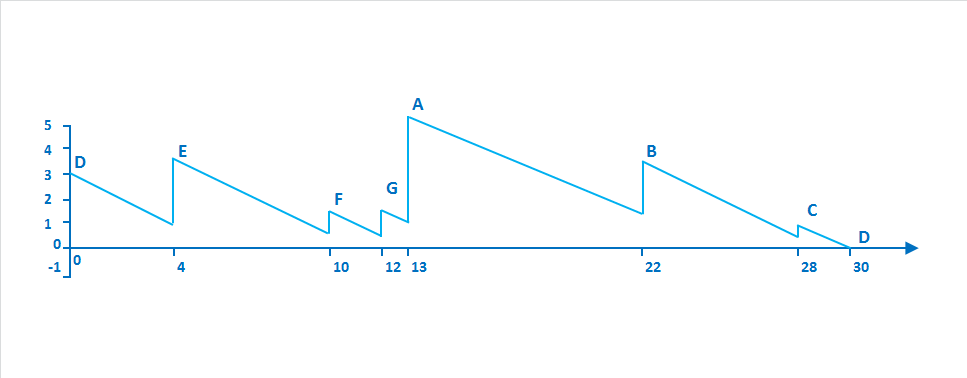
Ключ к решению: представьте, что перед въездом в каждый город вы записываете, сколько у вас осталось бензина перед заправкой. Назовем город с минимальным остатком X. Теперь давайте заправимся там полностью и начнем путешествие из этого минимального города. Если мы сможем вернуться в Х, не уйдя в минус, значит, мы нигде не остались без топлива, стало быть, запас топлива в нем был достаточным. Это условие и станет нашим инвариантом:

        import collections

KPL = 20  # Километров на литр 

def find_city(liters, distances, city_names):
    remaining_liters = 0
    CityAndRemainingFuel = collections.namedtuple('CityAndRemainingFuel',
                                                  ('city', 'remaining_liters'))
    city_remaining_fuel_pair = CityAndRemainingFuel(0, 0)
    num_cities = len(liters)
    
    for i in range(1, num_cities):
        remaining_liters += liters[i - 1] - distances[i - 1] // KPL
        if remaining_liters < city_remaining_fuel_pair.remaining_liters:
            city_remaining_fuel_pair = CityAndRemainingFuel(i, remaining_liters)
    
    return city_names[city_remaining_fuel_pair.city]

liters = [50, 20, 5, 30, 25, 10, 10]
distances = [900, 600, 200, 400, 600, 200, 100]
city_names = {
    0: 'A', 1: 'B', 2: 'C', 3: 'D', 
    4: 'E', 5: 'F', 6: 'G'
}

result = find_city(liters, distances, city_names)
print(f"Город, с которого нужно начать: {result}")

    

Вывод

        Город, с которого нужно начать: D
    

Временная сложность этого решения O(n), пространственная O(1).

Максимальный объем воды

Необходимо найти две линии, которые вместе с осью X образуют контейнер, способный удержать наибольшее количество воды.

Подходы к решению

Брутфорсный перебор за O(n2)

Проверяем все пары индексов (i, j), где i < j. Для каждой пары вычисляем объем воды: (j – i) * min(arr[i], arr[j]). Находим максимум среди всех вычисленных объемов.

Разделяй и властвуй

Разделяем массив на две половины. Решаем задачу для левой и правой половин отдельно. Находим максимум между элементами из левой и правой половин. Этот подход реализовать сложнее, чем брутфорсный, а временная сложность все равно остается O(n²).

Ключ к оптимальному решению: нужно начать с крайних элементов массива (0 и n-1). Вычисляем объем воды между ними, перемещаем указатель с меньшей высотой внутрь. Повторяем процесс, пока указатели не встретятся. Логика решения:

• Если arr[0] > arr[n-1], то любая комбинация n-1 с элементом правее 0 даст меньший объем. Поэтому мы можем сдвинуть правый указатель влево.
• Аналогично, если arr[0] < arr[n-1], мы сдвигаем левый указатель вправо.

        def get_max_trapped_water(arr):
    i, j, max_water = 0, len(arr) - 1, 0
    while i < j:
        width = j - i
        max_water = max(max_water, width * min(arr[i], arr[j]))
        if arr[i] > arr[j]:
            j -= 1
        else:  
            i += 1
    return max_water

arr = [1, 2, 1, 3, 4, 4, 5, 6, 2, 1, 3, 1, 3, 2, 1, 2, 4, 1]
result = get_max_trapped_water(arr)
print(f"Наибольший объем воды: {result}")
    

Вывод

        Наибольший объем воды: 48
    

Наибольший прямоугольник в силуэте

Имеется последовательность зданий, расположенных рядом друг с другом. Каждое здание имеет единичную ширину (например, 1 метр). Высота каждого здания задана целым числом. Эти здания формируют силуэт на горизонте. Необходимо найти площадь самого большого прямоугольника, который можно вписать в этот силуэт:

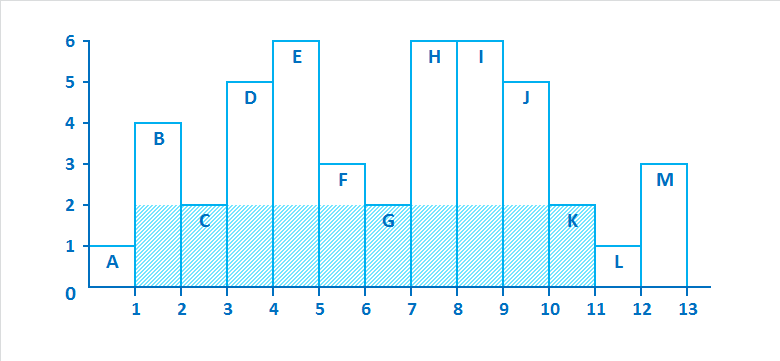
Решение

Это классическая задача на оптимизацию, для решения которой брутфорсные подходы оказываются слишком затратными:

Примитивный брутфорсный подход O(n³)

Для каждой пары зданий (i, j) находим минимальную высоту среди зданий от i до j. Умножаем эту высоту на ширину (j – i + 1), выбираем максимальную площадь из всех вычисленных. Для больших наборов данных это слишком медленное решение.

Улучшенный брутфорс O(n²)

Перебираем здания и для каждого из них находим наиболее удаленные слева и справа здания, не ниже текущего по высоте, что в итоге позволяет определить наибольший прямоугольник, поддерживаемый каждым зданием. Этот алгоритм работает быстрее, чем первый, но все равно он недостаточно хорош для больших объемов данных.

Оптимальный подход O(n)

Это решение использует стек для отслеживания активных опор (зданий, которые могут поддерживать прямоугольники) и работает следующим образом:

• Проходим по зданиям слева направо. Для каждого здания удаляем из стека здания, которые выше текущего, при удалении вычисляем площадь прямоугольника, поддерживаемого удаляемым зданием.
• Добавляем текущее здание в стек.
  
• После прохода всех зданий обрабатываем оставшиеся в стеке, считая правой границей конец массива.
  

Суть идеи:

• Стек всегда содержит здания в порядке возрастания высоты.
• Когда здание удаляется из стека, мы точно знаем правую границу его прямоугольника (текущий индекс).
  
• Левая граница – это позиция следующего здания в стеке (или начало, если стек пуст).
  

Составные элементы инварианта:

• Порядок высот – здания в стеке всегда расположены в порядке строго возрастающей высоты.
• Непрерывность – для любых двух соседних зданий в стеке не существует здания между ними (по индексу), которое было бы ниже, чем любое из этих двух.
• Активность – каждое здание в стеке является активной опорой, то есть потенциально может поддерживать наибольший прямоугольник, который еще не был заблокирован более низким зданием справа.
• Индексный порядок – здания в стеке всегда расположены в порядке возрастания их индексов (слева направо в исходном массиве).

        def calculate_largest_rectangle(heights):
    pillar_indices, max_rectangle_area = [], 0
    for i, h in enumerate(heights + [0]):
        while pillar_indices and heights[pillar_indices[-1]] >= h:
            height = heights[pillar_indices.pop()]
            width = i if not pillar_indices else i - pillar_indices[-1] - 1
            max_rectangle_area = max(max_rectangle_area, height * width)
        pillar_indices.append(i)
    return max_rectangle_area

heights = [1, 4, 2, 5, 6, 3, 2, 6, 6, 5, 2, 1, 3]
result = calculate_largest_rectangle(heights)
print(f"Наибольшая площадь прямоугольника: {result}")



    

Вывод:

        аибольшая площадь прямоугольника: 20
    

Временная сложность этого решения – O(n), так как каждое здание добавляется и удаляется из стека не более одного раза, пространственная – тоже O(n), в соответствии с максимальным размером стека, если, например, здания располагаются в порядке возрастания высоты.

В заключение

Рассмотренные выше примеры демонстрируют, что правильно выбранный инвариант может значительно упростить решение задачи и кратно улучшить производительность алгоритма. Умение находить такие инварианты требует практики и опыта, но это навык, который стоит затраченного времени: он пригодится не только для решения задач на собеседовании, но и для реальной разработки.

Статьи по теме

• 🅾️ Что такое «О» большое: объясняем на простых примерах
• 🐍🌳 Реализация алгоритма Укконена на Python
  
• 🏆👁️ Топовая задачка на Stack Overflow: как найти k пропущенных чисел в потоке данных