🏆👁️ Топовая задачка на Stack Overflow: как найти k пропущенных чисел в потоке данных

Хочешь уверенно проходить IT-интервью?

Мы понимаем, как сложно подготовиться: стресс, алгоритмы, вопросы, от которых голова идёт кругом. Но с AI тренажёром всё гораздо проще.

💡 Почему Т1 тренажёр — это мастхэв?

• Получишь настоящую обратную связь: где затык, что подтянуть и как стать лучше
• Научишься не только решать задачи, но и объяснять своё решение так, чтобы интервьюер сказал: "Вау!".
• Освоишь все этапы собеседования, от вопросов по алгоритмам до диалога о твоих целях.

Зачем листать миллион туториалов? Просто зайди в Т1 тренажёр, потренируйся и уверенно удиви интервьюеров. Мы не обещаем лёгкой прогулки, но обещаем, что будешь готов!

Реклама. ООО «Смарт Гико», ИНН 7743264341. Erid 2VtzqwP8vqy

Предыстория этой задачи изложена в первой части, в которой мы рассмотрели несколько вариантов решения для k = 1, 2 и 3, и выяснили, что для общего случая и для k ≥ 4 нужно использовать более универсальный подход, связанный с симметрическими функциями.

Таких подходов известно два, оба изложены в публикации Уильяма Гасарша (pdf), посвященной всем возможным способам вычисления k пропущенных чисел в массивах и потоках данных. В первом случае симметрические многочлены выводятся из степенных сумм с помощью тождеств Ньютона, а во втором случае симметрические функции используются на всех этапах решения. Любой из этих вариантов может претендовать на звание того самого «Святого Грааля», который хотел найти автор темы на Stack Overflow, но здесь мы будем рассматривать второй подход, как самый оригинальный.

«Святой Грааль»: aлгоритм сверки множеств

Гасарш приводит детальное математическое решение для общего случая, основанное на алгоритме Мински-Трахтенберга-Зиппеля. Условие задачи, принцип решения и последовательность действий выглядят так:

• Поток данных (или массив) представляет собой множество {1, 2...n}, в котором все числа уникальны, и могут быть расположены в любом порядке. При передаче множества k чисел были пропущены. Обозначим их y₁, y₂, ..., y_k. Необходимо найти эти числа, используя не более O(k log n) битов памяти.
• Чтобы соблюсти ограничение по использованию памяти (и реализовать поточную обработку), мы вычисляем симметрические функции для каждого числа x₁, x₂, ..., x_n-k по мере поступления чисел. По определению, s₀ всегда равна 0, s₁ представляет собой сумму чисел, s₂ – сумму произведений всех возможных пар чисел, s₃ – сумму произведений всех комбинаций троек чисел и так далее. В итоге мы получим набор симметрических функций, которые в нотации Гасарша обозначаются s₁^n-k, s₂^n-k, s₃^n-k и так далее (L – длина фактически полученной последовательности чисел, то есть n – k).

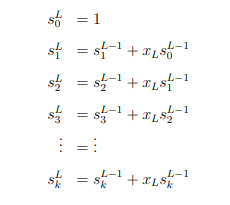
• Зная L и k, мы получаем n – длину полной числовой последовательности. Это дает нам возможность вычислить симметрические суммы для полной последовательности, с учетом всех чисел, которые пропущены в фактическом потоке данных. Эти вычисления делаются независимо от входного потока:

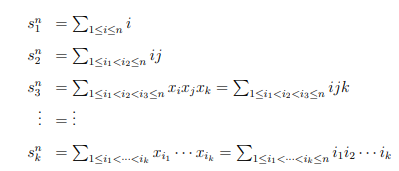
• В результате мы получаем систему уравнений, из которых можем вывести сумму, произведение и суммы произведений всех возможных комбинаций пропущенных чисел, поскольку у нас уже есть s_iⁿ , s_i^n-k , s₀^k , s₀^n−k :

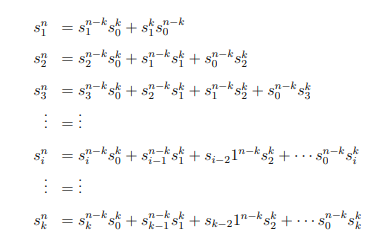
• Итогом всех этих манипуляций станет полином k-степени. Вычислив его корни, мы найдем все пропущенные числа:

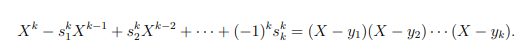
Как быстро освоить математику?

Заглядывай на наш онлайн-курс по математике для Data Science, где ты познакомишься с основными моделями машинного обучения, научишься выбирать и применять подходящие tree-based модели.

Программа занятий:

• Школьная математика: от теории множеств до производной и интеграла.
• Математический анализ: от числовых последовательностей до теории меры и интеграла Ламбера.
• Линейная алгебра: от матриц до билинейных форм.
• Комбинаторика: правила комбинаторики, множества и сочетания.
• Теория вероятностей и математическая статистика: от случайных событий до регрессии.
• Машинное обучение: Word2vec, градиентный спуск, KNN и т. д.

Реализация алгоритма на Python

Функция actual_sums() вычисляет фактические симметрические функции по мере поступления чисел:

        def actual_sums(lst, k):
    sums = [0] * (k + 1)
    sums[0] = 1  # s0 по определению равна 1

    for num in lst:
        for j in range(k, 0, -1):
            sums[j] += num * sums[j - 1]

    return sums
    

Функция complete_sums() работает независимо от входного потока данных, поскольку вычисляет ожидаемые, полные симметрические функции:

        def complete_sums(n, k):
    sums = [0] * (k + 1)
    sums[0] = 1  # s0 по определению равна 1

    for i in range(1, n + 1):
        for j in range(k, 0, -1):
            sums[j] += i * sums[j - 1]

    return sums
    

Коэффициенты полинома, как и ожидаемые/фактические суммы, вычисляются рекуррентно:

        def compute_coeff(actual, complete, k):
    coeffs = [0] * (k + 1)
    coeffs[0] = 1
    coeffs[1] = complete[1] - actual[1]

    for i in range(2, k + 1):
        coeff = complete[i] - actual[i]
        for j in range(1, i):
            coeff -= actual[j] * coeffs[i - j]
        coeffs[i] = coeff

    return coeffs
    

К примеру, для числовой последовательности, в которой пропущено 12 чисел, коэффициенты полинома будут выглядеть так:

        #lst = [22, 15, 4, 24, 14, 2, 17, 8, 28, 20, 5, 10, 12, 1, 19, 26]
#k = 12

[1, 179, 14336, 678200, 21069782, 451977986, 6849635572, 73706941164, 557311879377, 2877528115395, 9587151599652, 18393142628196, 15226233422400]
    

Решать такие уравнения проще всего с NumPy:

        import numpy as np

def complete_sums(n, k):
    sums = [0] * (k + 1)
    sums[0] = 1  # s0 по определению равна 1

    for i in range(1, n + 1):
        for j in range(k, 0, -1):
            sums[j] += i * sums[j - 1]

    return sums

def actual_sums(lst, k):
    sums = [0] * (k + 1)
    sums[0] = 1  # s0 по определению равна 1

    for num in lst:
        for j in range(k, 0, -1):
            sums[j] += num * sums[j - 1]

    return sums

def compute_coeff(actual, complete, k):
    coeffs = [0] * (k + 1)
    coeffs[0] = 1
    coeffs[1] = complete[1] - actual[1]

    for i in range(2, k + 1):
        coeff = complete[i] - actual[i]
        for j in range(1, i):
            coeff -= actual[j] * coeffs[i - j]
        coeffs[i] = coeff

    return coeffs

lst = [22, 15, 4, 24, 14, 2, 17, 8, 28, 20, 5, 10, 12, 1, 19, 26]
k = 12
n = len(lst) + k

actual = actual_sums(lst, k)
complete = complete_sums(n, k)
coefficients = compute_coeff(actual, complete, k)
roots = np.roots(coefficients)
print("Пропущенные числа:")
for root in roots:
    print(f"{root* -1:.0f}")
    

Результат:

        Пропущенные числа:
27
25
23
21
18
16
13
11
9
7
6
3
    

Подведем итоги

Алгоритм сверки множеств позволяет обойтись без тождеств Ньютона и чисел Бернулли, поскольку он основан на прямом вычислении симметрических функций. Оптимальная производительность достигается за счет рекуррентного подхода: в противном случае, вычисление всех возможных комбинаций пар, двоек, троек, k-наборов для всей последовательности сразу привело бы к временной сложности O(n^k).

Статьи по теме

• 🤯 Как простая задачка поставила в тупик программистов (и как они из него выбрались)
  
• 🅾️ Что такое «О» большое: объясняем на простых примерах
  
• 🐍🌳 Реализация алгоритма Укконена на Python