Если хочешь подтянуть свои знания, загляни на наш курс «Алгоритмы и структуры данных», на котором ты:
- углубишься в решение практических задач;
- узнаешь все про сложные алгоритмы, сортировки, сжатие данных и многое другое.
Ты также будешь на связи с преподавателем и другими студентами.
В итоге будешь браться за сложные проекты и повысишь чек за свою работу 🙂
В программировании мы постоянно работаем с наборами данных – однотипных (статистические числовые показатели за разные годы) или логически связанных друг с другом (сведения о пользователе вашего приложения – имя, возраст, почтовый адрес).
Другие статьи цикла:
- Часть 2. Стеки, очереди и связные списки
- Часть 3. Деревья
- Часть 4. Графы
- Часть 5. Объекты и хеширование
- Часть 6. Полезные алгоритмы для веб-разработки
Чтобы с данными было удобнее работать, мы организовываем их в структуры.
Структура обеспечивает удобное представление данных, а чтобы работать с ними мы используем алгоритмы.
Некоторые алгоритмы встроены в структуры данных, являются их частью. Обычно это базовые алгоритмы работы с данными, у которых нет многочисленных вариаций. Например, массив предоставляет алгоритмы добавления и удаления элементов. Другие алгоритмы, более сложные, обычно реализуются поверх структур. Например, разнообразные способы поиска и упорядочивания данных.
Зачем нужны разные структуры и алгоритмы?
Одно и то же действие можно сделать с помощью разных алгоритмов. Например, для обычной сортировки массивов существует десятки разных вариантов, а мы используем метод Array.prototype.sort и даже не знаем о них).
Зачем нужно все это многообразие?
Для каждой задачи есть свой идеальный инструмент. Можно, конечно, забивать гвозди утюгом, но молоток для этого подойдет лучше. И это совсем не значит, что утюг хуже молотка – просто он решает другие задачи. То же и с алгоритмами и структурами данных. Одну и ту же задачу можно решить разными способами, но обычно среди них находится парочка более эффективных, более быстрых – лучших.
Разные подходы к решению задач
Алгоритмов, конечно, много, но в основе каждого из них обычно лежит один из основных подходов к решению задач. Этих подходов уже значительно меньше. Самые популярные из них:
- Полный перебор.
- Разделяй и властвуй.
- Динамическое программирование.
- Жадные алгоритмы.
Если вы разберетесь в этих подходах, то сможете намного свободнее оперировать алгоритмами, даже не изучая их детально. Ведь понять идею намного важнее, чем выучить ее реализацию.
Полный перебор (brute force)
Это решение в лоб, заключающееся в переборе всех возможных вариантов. Таким образом мы действуем в магазине одежды, перебирая все рубашки на вешалке в поиске подходящей.
Примером алгоритма полного перебора является линейный поиск значения в массиве.
Разделяй и властвуй (divide and conquer)
Если задачу можно разделить на более мелкие части, то нужно ее разделить, и продолжать делить, пока это будет возможным. Потом решить задачу для каждой части и объединить полученные результаты при необходимости.
Примеры стратегии "разделяй и властвуй": двоичный поиск и сортировка массива слиянием.
Динамическое программирование (dynamic programing)
Суть динамического программирования такая же, как у "разделяй и властвуй": разделение большой задачи на подзадачи. Два этих подхода в целом похожи, но имеют важные различия. Динамическое программирование в некотором смысле расширяет "разделяй и властвуй" и применяется для более узкого набора проблем.
Прекрасным примером проблемы, решаемой с помощью динамического программирования, является вычисление чисел Фибоначчи.
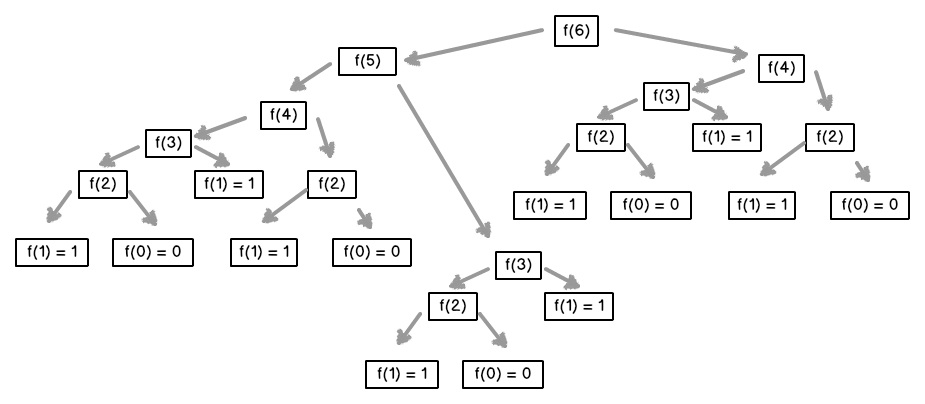
Чтобы найти шестое число в ряду, нам нужно найти сначала пятое и четвертое, то есть разделить задачу на более мелкие. При этом можно кешировать и повторно использовать результаты вычисления более мелких чисел – первого, второго и т.д.
Жадные алгоритмы (greedy algorithms)
Более сложный подход к решению проблем предполагает на каждом локальном этапе принятие решений, которые на данный момент являются оптимальными. Допускается, что конечное решение тоже будет оптимальным.
Требуется выдать конкретную сумму минимально возможным количеством монет разного достоинства (10 рублей, 5 рублей, 2 рубля, 1 рубль). Сначала набираем максимально возможную сумму монетами самого высокого достоинства (10 рублей). Потом переходим к пяти-рублевым и пытаемся набрать ими остаток и так далее.
Вычислительная сложность алгоритмов
Разные алгоритмы имеют разную эффективность. Например, очевидно, что если искомый элемент находится в самом конце массива, то метод полного перебора потребует больше времени, чем стратегия "разделяй и властвуй".
Также при оценке сложности следует учитывать дополнительное использование памяти, например, создание временных переменных.
В измерении вычислительной сложности алгоритмов полезно разобраться, чтобы использовать более эффективные.
Подробнее о нотации O-большое:
- Асимптотическая сложность алгоритмов: что за зверь?
- Анализ алгоритмов для начинающих: вводное руководство
Какие алгоритмы нужно знать, чтобы стать хорошим программистом?
В крайнем случае вы всегда можете найти нужный алгоритм в гугле, но для этого нужно хотя бы знать, что искать.
Для развития алгоритмической смекалки мы начнем с базовых структур и алгоритмов, а затем перейдем к более сложным.
Массивы
Описание структуры и основные операции
Массив в JavaScript – это самая простая упорядоченная коллекция элементов. Каждый элемент массива имеет свой порядковый номер (индекс), нумерация начинается с нуля. Таким образом, у массива есть начало (индекс 0) и конец.
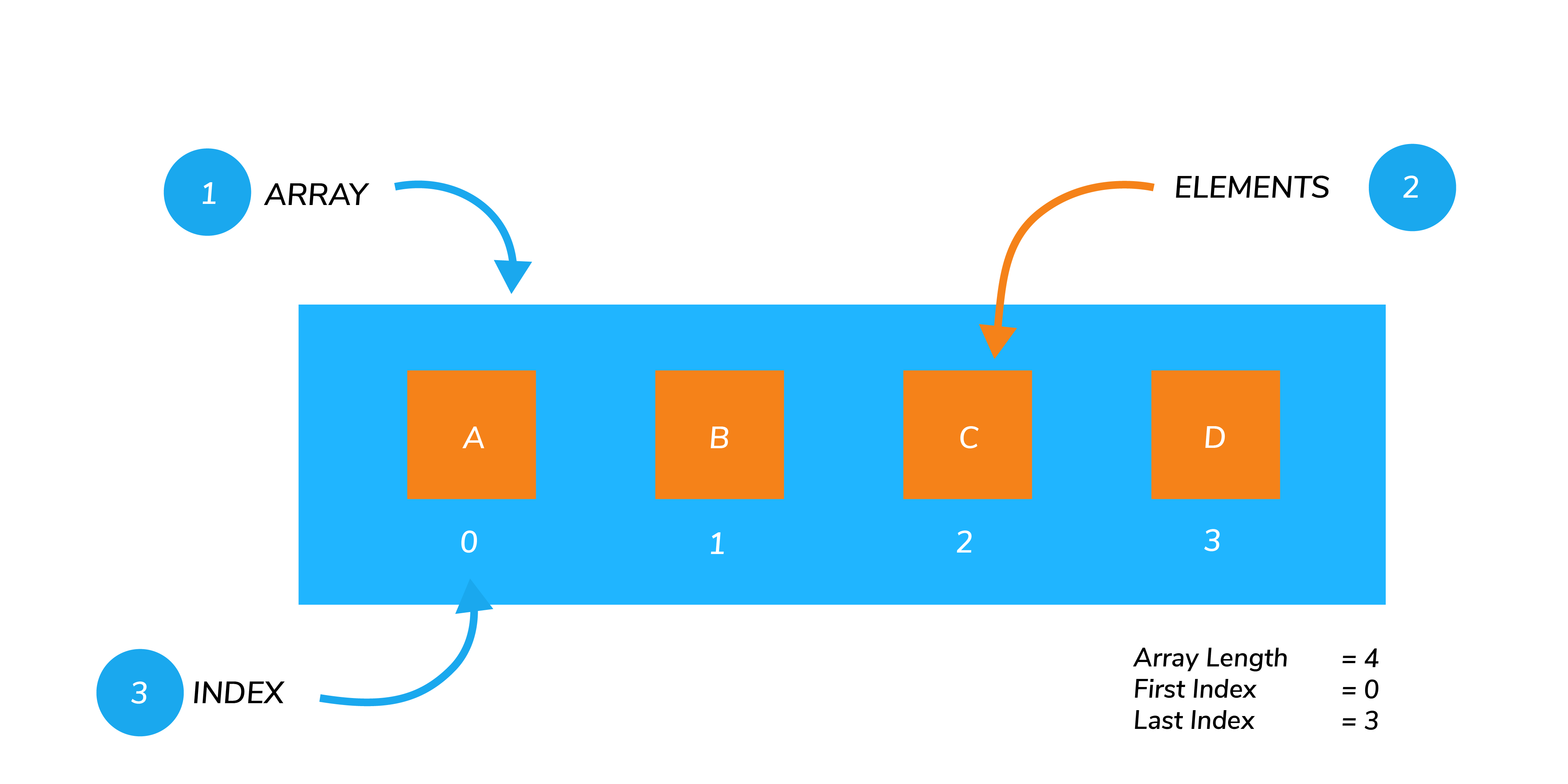
Так как массивы упорядочены, к каждому элементу массива можно обратиться по его индексу – это прямое обращение. Если вы хотите узнать, какой элемент стоит в массиве на третьем месте, вам не придется перебирать сначала первый и второй.
- Array.prototype.push – вставка элемента (элементов) в конец массива.
- Array.prototype.pop – удаление элемента из конца массива.
Это очень простые алгоритмы: они изменяют только длину массива, а нумерация предыдущих элементов остается прежней.
- Array.prototype.unshift – вставка элемента (элементов) в начало массива.
- Array.prototype.shift – удаление элемента из начала массива.
Казалось бы, почти то же самое, однако эти алгоритмы уже существенно сложнее. Если вы производите добавляете или удаляете элементы в начале массива, необходимо изменить нумерацию всех последующих элементов.
Производительность
Если в массиве 5 элементов, и вы добавляете в начало ещё один, то кроме непосредственно вставки нового элемента, нужно перебрать пять старых и изменить индекс каждого из них. Это пять дополнительных действий.
1.Вставить новый элемент в позицию 0
2.Взять следующий элемент с индексом 0 и изменить его на 1
3.Взять следующий элемент с индексом 1 и изменить его на 2
…
6.Взять последний элемент с индексом 4 и изменить его на 5
Если же в исходном массиве было 5000 элементов, придется произвести 5000 дополнительных действий. Чем больше элементов, тем больше действий – это пример полного перебора.
Зная о подобных особенностях работы алгоритмов, вы сможете писать более эффективный код.
Сложность базовых операций в массиве
| Получение элемента | 1 (константное время, не зависит от кол-ва элементов) |
| Вставка в конец массива | 1 |
| Вставка в начало массива | n (прямая зависимость от кол-ва элементов) |
| Удаление из конца массива | 1 |
| Удаление из начала массива | n |
Алгоритмы сортировки массивов
Операции добавления элементов в массив и удаления из него довольно простые и понятные. Давайте займемся чем-нибудь посложнее, например, сортировкой.
Сортировка массивов производится в программировании очень часто, например, если мы сортируем строки по алфавиту для различных справочников. С отсортированными данными намного проще работать, в частности в отсортированном массиве проще искать нужный элемент (вспомните пример поиска слова в словаре – это отсортированный массив).
JavaScript предоставляет нам готовый метод для решения этой задачи – Array.prototype.sort. Этот метод принимает функцию для попарного сравнения двух элементов, потом происходит магия – и массив уже отсортирован. А что внутри этого черного ящика? Как именно происходит упорядочивание?
Мы разберем пять из них:
- пузырьковую сортировку;
- сортировку выбором;
- сортировку вставками;
- сортировку слиянием;
- быструю сортировку.
Сравнение элементов и устойчивость сортировки
Каждый из этих алгоритмов использует попарное сравнение элементов, чтобы определить, какой из них должен идти раньше. Именно для этого используется функция, которую мы передаем в метод sort. В примерах мы будем иметь дело с массивами чисел, поэтому в качестве функции-компаратора (сравнителя) будем использовать следующую:
const comparator = (a, b) => a - b;
- Если
aбольшеb, то вернется положительное число. Это значит, чтоaдолжно стоять в массиве послеb. - Если
aменьшеb, то вернется отрицательное число, иaдолжно находиться доb. - Если
aиbравны, то вернется 0. В этом случае порядок элементов может сохраниться, а может и поменяться. Глобально это не повлияет на задачу сортировки, но может иметь различные побочные эффекты.
Различают устойчивые и неустойчивые алгоритмы. Первые не изменяют порядок элементов, а вторые могут его изменять.
Перестановка элементов
Еще одна вспомогательная функция, которая нам потребуется – функция перестановки двух элементов. Она просто меняет местами элементы массива с указанными индексами:
const swap = (arr, i, j) => {
let temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
Для перестановки мы используем временную переменную temp, но можно обойтись и без нее, воспользовавшись синтаксисом деструктуризации:
const swap = (arr, i, j) => [arr[i], arr[j]] = [arr[j], arr[i]]
Пузырьковая сортировка
Один из самых простых алгоритмов сортировки.
Легко догадаться, что в результате таких манипуляций самое больше число окажется в конце массива. Оно всплывет, как пузырек в воде, отсюда и название сортировки.
Осталось лишь повторить всю последовательность действий, пока не всплывут все элементы.
Реализация на JavaScript:
function bubbleSort(arr) {
for (let j = arr.length - 1; j > 0; j--) {
for (let i = 0; i < j; i++) {
if (comparator(arr[i], arr[i+1]) > 0) {
swap(arr, i, i+1);
}
}
}
}
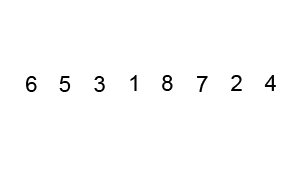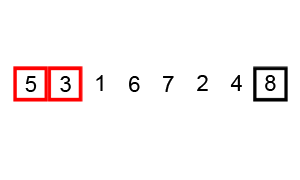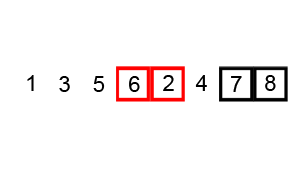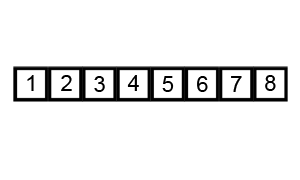
- Первый цикл отслеживает индекс последнего всплывшего элемента. На каждой итерации он будет уменьшаться.
- Второй цикл – это индекс активного элемента на текущей итерации. Он будет начинаться с нуля и продолжаться до элементов, "всплывших" на предыдущих итерациях. Так как они уже отсортированы, не имеет смысла снова их сравнивать.
Сложность:
Пузырьковая сортировка является устойчивой, а ее временная сложность составляет O(N²) в худшем случае. Это означает, что для массива с n элементами нужно совершить n2 операций: для каждого из элементов приходится сделать проход по всем остальным элементам массива. Реальное значение чуть меньше чем n2 , но при расчете сложности алгоритма все коэффициенты отбрасываются. В лучшем случае, если массив уже отсортирован, потребуется всего n операций.
Сортировка выбором
Этот алгоритм похож на сортировку пузырьком: он на каждой итерации отсортировывает один элемент, только собираются они не в конце массива, а в начале.
Реализация на JavaScript:
function selectionSort(arr) {
for (let i = 0; i < arr.length - 1; i++) {
let min = i;
for (let j = i + 1; j < arr.length; j++) {
if (comparator(arr[min], arr[j]) > 0) {
min = j;
}
}
if (min !== i) swap(arr, i, min);
}
}
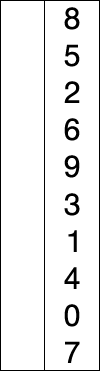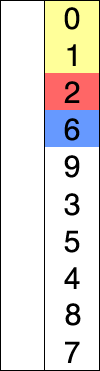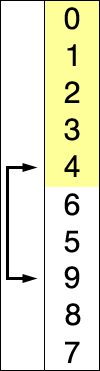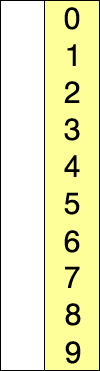
Начинаем с нулевого элемента. На каждой итерации ищем минимум в неотсортированной части и добавляем его к отсортированной.
Сложность:
В отличие от пузырьковой, сортировка выбором неустойчива, но сложность у нее такая же – O(N²).
Сортировка вставками
Реализация на JavaScript:
function insertionSort(arr) {
for (let i = 1; i < arr.length; i++) {
let current = i;
while(arr[current - 1] !== undefined && comparator(arr[current], arr[current - 1]) < 0) {
swap(arr, current - 1, current);
current--;
}
}
}
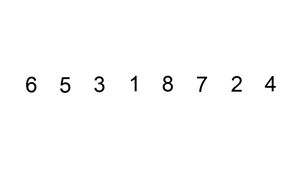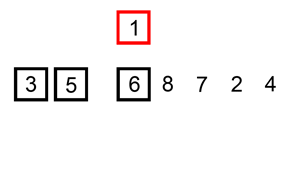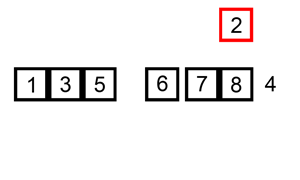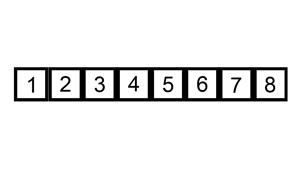
Начинаем с первого элемента (нулевой считаем отсортированным). На каждой итерации сравниваем активный элемент с отсортированными и находим его место.
Сложность:
Сложность сортировки вставками такая же, как у предыдущих алгоритмов – O(N²) в худшем случае (если массив отсортирован в обратном порядке). Алгоритм является стабильным.
Сортировка слиянием
Сортировка слиянием – отличный пример применения стратегии "разделяй и властвуй".
Алгоритм состоит из трех этапов:
- Исходный массив разделяется на две примерно равные части.
- Каждая часть сортируется отдельно.
- Обе отсортированные части объединяются в один массив.
На третьем этапе тоже загадка – как именно происходит объединение двух частей в один массив. Тут все довольно просто: на каждом шаге мы берем первые элементы массивов, сравниваем их, выбираем меньший и добавляем в новый объединенный массив.
Реализация на JavaScript:
function mergeSort(arr) {
if (arr.length <= 1) return arr;
// середина массива
let middle = Math.floor(arr.length / 2);
// два подмассива, которые будут сортироваться отдельно
let left = arr.slice(0, middle);
let right = arr.slice(middle);
// слияние отсортированных подмассивов
return mergeSortedArrays(mergeSort(left), mergeSort(right));
}
function mergeSortedArrays(arr1, arr2) {
// Результат слияния
let newArray = [];
// текущие индексы сравниваемых элементов
let index1 = 0;
let index2 = 0;
// сравнение активных элементов
while(index1 < arr1.length && index2 < arr2.length) {
let min = null;
if (comparator(arr1[index1], arr2[index2]) <= 0) {
min = arr1[index1]; // добавление минимального элемента в массив
index1++; // сдвиг индекса активного элемента первого массива
} else {
min = arr2[index2];
index2++;
}
newArray.push(min);
}
return [...newArray, ...arr1.slice(index1), ...arr2.slice(index2) ];
}
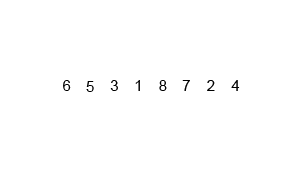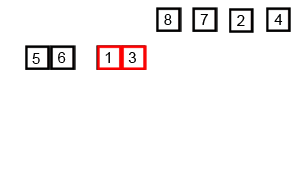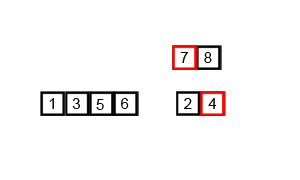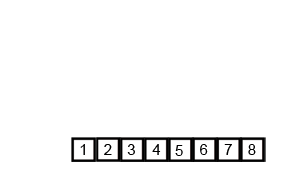
Основная функция сортировки mergeSort делит массив на две части с помощью метода Array.prototype.slice, отправляет каждую часть на рекурсивную сортировку, а затем снова объединяет их с помощью функции mergeSortedArrays.
Вспомогательная функция mergeSortedArrays начинает с нулевых элементов обоих массивов, сравнивает их и находит минимальный. Для того массива, в котором нашелся минимум, активный индекс сдвигается вправо. Сравнения происходят пока один из массивов не закончится, тогда остаток другого просто присоединяется к результирующему массиву.
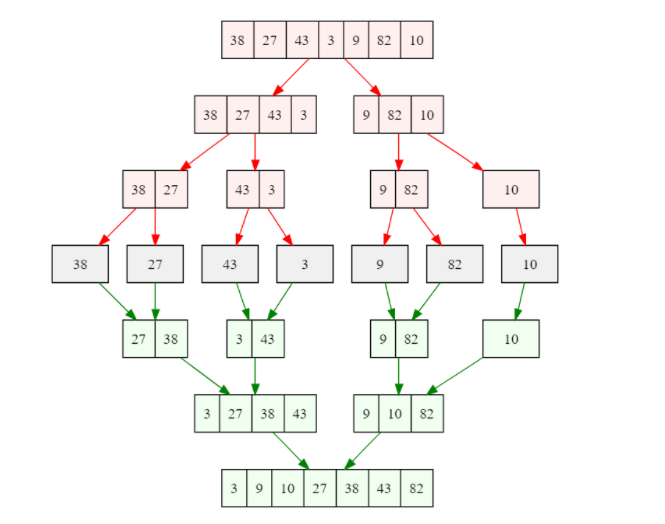
Сложность:
Сортировка слиянием является стабильной. Для нее требуется выполнить n * log(n) операций. Это эффективнее, чем предыдущие алгоритмы.
Быстрая сортировка
Алгоритм быстрой сортировки (сортировка Хоара), как ни странно, является одним из самых быстрых алгоритмов сортировки. Он немного похож и на пузырьковую сортировку, и на сортировку слиянием, так как тоже использует стратегию "разделяй и властвуй".
- Сначала в массиве выбирается опорный элемент (пивот). Выбрать его можно любым способом: например, взять первый, средний или случайный элемент. От способа выбора во многом зависит эффективность алгоритма.
- Затем все остальные элементы сравниваются с опорным и переставляются так, чтобы все элементы, которые меньше опорного оказались до него, а все, которые больше – после. Под больше и меньше здесь имеется в виду результат сортировки. На этом этапе в массиве сначала идут все элементы меньше опорного (для которых компаратор вернул отрицательное число), затем опорный, а затем все элементы больше опорного (компаратор вернул положительное число).
- И наконец для групп "меньше" и "больше" рекурсивно выполняется тот же самый алгоритм. Сам опорный элемент может быть включен в одну из групп.
Реализация на JavaScript:
function quickSort(arr, start, end) {
if (start === undefined) start = 0;
if (end === undefined) end = arr.length - 1;
if (start >= end) return;
// индекс опорного элемента
let pivot = partition(arr, start, end);
// рекурсивная сортировка подмассивов
quickSort(arr, start, pivot - 1);
quickSort(arr, pivot + 1, end);
}
function partition(arr, start, end) {
// Берем в качестве опорного последний элемент подмассива
let pivotValue = arr[end];
// изначально считаем, что pivotValue минимальное значение
// и должно находиться в начале массива
let pivotIndex = start;
// перебираем все элементы
for (let i = start; i < end; i++) {
// значения меньше опорного перемещаем перед ним
if (comparator(arr[i], pivotValue) < 0) {
swap(arr, i, pivotIndex);
pivotIndex++;
}
}
// ставим опорный элемент в нужное место
swap(arr, pivotIndex, end);
return pivotIndex;
}
Функция quickSort принимает в качестве аргументов сам массив, а также начальную и конечную позиции, между которыми нужно произвести перестановки (границы подмассива). При первом вызове start и end не указываются, поэтому сортировка происходит для всего массива. При каждом рекурсивном вызове start и end приближаются друг к другу, так как подмассивы уменьшаются.
Вспомогательная функция partition также принимает исходный массив и границы подмассива для сортировки. Она находит опорный элемент для этого подмассива и перемещает остальные элементы согласно алгоритму, а затем возвращает индекс опорного элемента для дальнейшей рекурсивной сортировки.
Помимо рекурсии быструю сортировку можно реализовать итеративно (с помощью циклов). Также существует огромное количество модификаций алгоритма быстрой сортировки, направленных на улучшение ее эффективности, например, различные вариации выбора опорного элемента.
Сложность:
В худшем случае при неудачном выборе пивота быстрая сортировка массива имеет сложность O(n2), однако в среднем она равна n * log(n) и является одной из самых эффективных.
Это нестабильная сортировка.
Сложность разных алгоритмов сортировок
| Алгоритм | Лучший случай | Средний случай | Худший случай |
| Сортировка пузырьком | n | n2 | n2 |
| Сортировка выбором | n2 | n2 | n2 |
| Сортировка вставками | n | n2 | n2 |
| Сортировка слиянием | n log(n) | n log(n) | n log(n) |
| Быстрая сортировка | n log(n) | n log(n) | n2 |
Array.prototype.sort, то есть изменяют его. Чтобы обойтись без мутаций, вы должны создать копию исходного массива и производить все операции с ней.Какой же алгоритм сортировки используется в Array.prototype.sort? Спецификация этого не определяет, поэтому каждый браузер сам решает. Вот небольшое интересное исследование на эту тему (от 2016 года).
Больше сортировок, хороших и разных:
- Какая сортировка самая быстрая? Тестируем алгоритмы
- Сортировки в гифках: 8 самых популярных алгоритмов
Алгоритмы поиска в массиве
JavaScript предлагает несколько встроенных методов для ее решения:
Как же происходит поиск? Рассмотрим два алгоритма, использующих два разных подхода.
Сравнение элементов
Важной частью алгоритмов поиска также является функция-компаратор, которая собственно и определяет, какой элемент является искомым. Поскольку мы продолжаем работать с числовыми массивами, наш компаратор будет очень простым:
const comparator = (value, wantedValue) => value - wantedValue
По сути он не изменился с предыдущей задачи:
- если вернётся 0, значит, числа равны;
- если отрицательное число, значит, значение меньше искомого;
- если положительное число, значит, значение больше искомого.
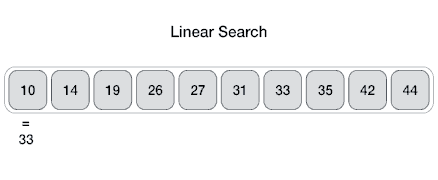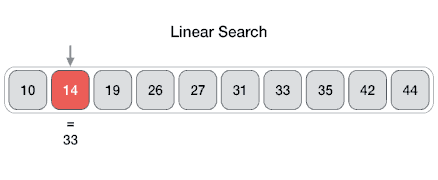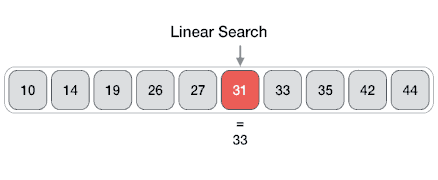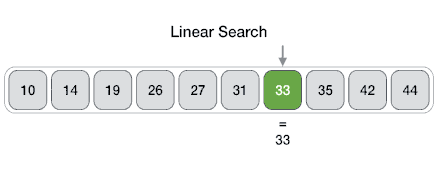
Линейный поиск (полный перебор)
Как следует из названия, этот алгоритм просто перебирает все элементы массива по порядку и для каждого из них вызывает компаратор. Именно так и работают перебирающие методы массивов, например, Array.prototype.find.
Реализация на JavaScript могла бы выглядеть вот так:
function linearSearch(arr, wanted) {
let found = [];
arr.forEach((el, i) => {
if (comparator(el, wanted) === 0) found.push(i);
};
return found;
}
Функция linearSearch находит все подходящие элементы в отличие от Array.prototype.find, которая ограничивается только первым. Очевидно, что сложность этого алгоритма равна O(n), так как в худшем случае придется перебрать каждый элемент массива.
Бинарный поиск (разделяй и властвуй)
Второй алгоритм поиска использует принцип разделяй и властвуй и является более эффективным. Вот только ему для работы непременно нужен отсортированный массив, иначе ничего не получится.
Реализация на JavaScript:
function binarySearch(arr, wanted) {
// Границы подмассива для поиска
let start = 0;
let end = arr.length - 1;
while (start <= end) {
// центр подмассива
let middle = start + Math.floor((end - start) / 2);
if (comparator(arr[middle], wanted) === 0) return middle;
// выбираем нужную половину
if (comparator(arr[middle], wanted) < 0) start = middle + 1;
else end = middle - 1;
}
return -1; // ничего не нашлось
}
Сложность этого алгоритма составляет O(log(n)), но не забывайте, что ему требуется предварительная сортировка.
Заключение
Итак, мы разобрались с основными понятиями, поближе познакомились со встроенными в JavaScript массивами и даже реализовали 7 популярных алгоритмов для работы с ними. В следующей статье цикла перейдем к более сложным структурам и алгоритмам.



Комментарии