Если хочешь подтянуть свои знания, загляни на наш курс «Алгоритмы и структуры данных», на котором ты:
- углубишься в решение практических задач;
- узнаешь все про сложные алгоритмы, сортировки, сжатие данных и многое другое.
Ты также будешь на связи с преподавателем и другими студентами.
В итоге будешь браться за сложные проекты и повысишь чек за свою работу 🙂
Продолжаем изучать популярные алгоритмы и структуры данных и их реализацию на JavaScript. В предыдущей статье мы разобрались с деревьями – нелинейными иерархическими структурами. В этой копнем еще глубже и познакомимся со старшими братьями деревьев – графами.
Другие статьи цикла:
- Часть 1. Основные понятия и работа с массивами
- Часть 2. Стеки, очереди и связные списки
- Часть 3. Деревья
- Часть 5. Объекты и хеширование
- Часть 6. Полезные алгоритмы для веб-разработки
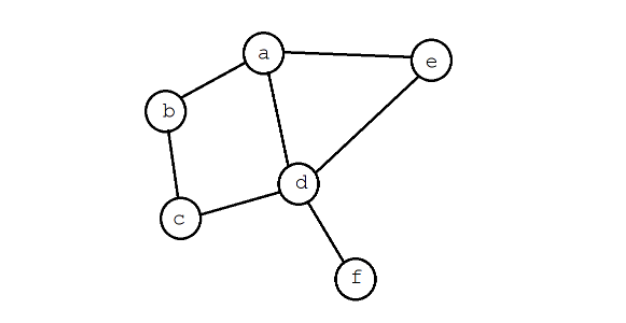
Количество вершин определяет порядок графа, а количество ребер – его размер.
Если две вершины графа соединены одним ребром, они называются соседними, или смежными. В графе также могут быть отдельно стоящие вершины, не связанные с другими, они называются изолированными. Количество ребер, исходящих из вершины, определяют ее степень связности.
Значение и применение структуры
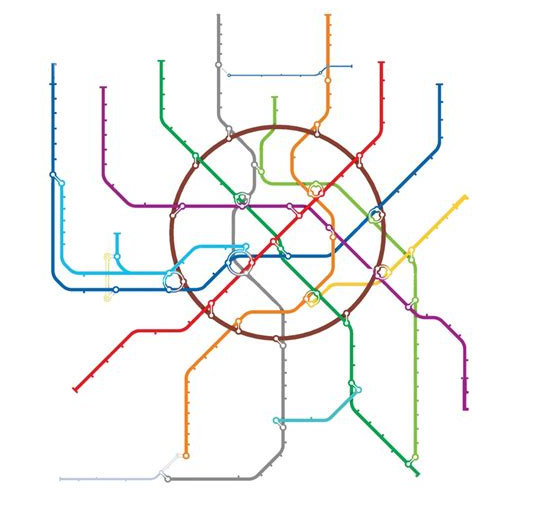
Основная задача графа – отображать связи (ребра) между разными сущностями (вершины). Самый простой пример – карта метро, на которой станции являются вершинами графа, а связывающие их перегоны – ребрами.
Деревья, которые мы разбирали в предыдущей части цикла, также являются графами.
С помощью графов можно представить связи между пользователями социальной сети (подписки) или ссылки между разными страницами одного сайта (перелинковка). В таких графах ребра будут иметь направление – пользователь А подписан на пользователя Б, а не наоборот. Это ориентированные графы.
В настоящее время это очень востребованная структура данных, так как она позволяет работать с большими объемами плохо структурированной информации. На графах, например, основываются разнообразные системы рекомендаций и ранжирования контента.
Способы представления графов в JavaScript
Итак, зачем нужны графы, разобрались, но остается неясным, как их использовать. В JavaScript мы не можем просто нарисовать несколько вершин и соединить их ребрами – нужен какой-то способ представления.
Список смежности
При его составлении для ориентированного графа важно учитывать направление ребер.
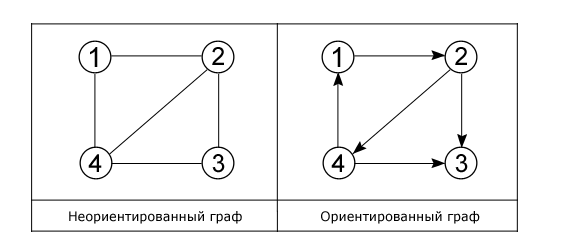
Для первого (неориентированного) графа список смежности будет выглядеть так:
const graph = {
1: [2,4],
2: [1,3,4],
3: [2,4]
4: [1,2,3]
}
Мы представили его в виде JavaScript-объекта с четырьмя свойствами, каждое из которых соответствует вершине графа. В качестве значений – массивы смежных вершин:
- из вершины 1 можно попасть в 2 и 4;
- из вершины 2 можно попасть в 1, 3 и 4;
- из вершины 3 можно попасть в 2 и 4;
- из вершины 4 можно попасть в 1, 2, 3.
Ориентированный граф выглядит почти так же, но список смежности у него другой:
const graph = {
1: [2],
2: [3,4],
3: [],
4: [1,3]
}
Из вершины 3 не выходит ни одно ребро, поэтому из нее нельзя никуда попасть – ее массив смежных вершин пуст.
Матрица смежности
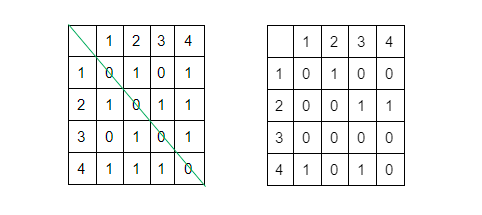
Связь определяется построчно. Первая строка соответствует вершине 1, нужно определить, есть ли путь из нее в вершины, представленные столбцами таблицы.
У неориентированного графа матрица смежности симметрична, а у ориентированного – нет.
На JavaScript граф можно представить в виде двумерного массива:
const graph = [
[ 0, 1, 0, 0 ],
[ 0, 0, 1, 1 ],
[ 0, 0, 0, 0 ],
[ 1, 0, 1, 0 ],
]
Сравнение способов
Список смежности – более компактный способ представления графа, он требует меньше памяти и особенно удобен для "разреженных" графов, у которых немного ребер.
В то же время матрица – более наглядная и удобная структура, позволяющая быстро определить, есть ли связь между двумя вершинами. Для "плотных" графов с большим количеством ребер матрица обычно выгоднее, чем список.
Например, операция проверки наличия связи между двумя вершинами a и b в матрице занимает константное время – достаточно лишь проверить элемент graph[a][b]. В списке смежности же это будет сложнее – потребуется поиск элемента b в массиве graph[a].
Помимо списка и матрицы смежности можно использовать и более абстрактные представления, например, хранить отдельно множество вершин и отдельно множество ребер.
Реализация на JavaScript
Напишем класс для самого простого неориентированного графа с хранением данных в виде списка смежности.
class Graph {
constructor() {
this.vertices = {}; // список смежности графа
}
addVertex(value) {
if (!this.vertices[value]) {
this.vertices[value] = [];
}
}
addEdge(vertex1, vertex2) {
if (!(vertex1 in this.vertices) || !(vertex2 in this.vertices)) {
throw new Error('В графе нет таких вершин');
}
if (!this.vertices[vertex1].includes(vertex2)) {
this.vertices[vertex1].push(vertex2);
}
if (!this.vertices[vertex2].includes(vertex1)) {
this.vertices[vertex2].push(vertex1);
}
}
}
Основные методы графа:
addVertex– добавление новой вершины;addEdge– добавление нового ребра.
Так как граф неориентированный, новое ребро является двусторонней связью, поэтому мы добавляем новые записи в списки обеих смежных вершин. Для ориентированного графа нужно лишь немного изменить метод addEdge, чтобы новая связь шла лишь в одном направлении.
Основные алгоритмы на графах
Мы разберем лишь две востребованные в программировании задачи: обход графа (в т.ч. поиск в графе) и нахождение кратчайшего пути между двумя вершинами.
Обход графа
Как и в случае с деревьями, у нас есть два способа обхода графов с разным порядком перебора вершин: поиск в ширину и поиск в глубину. Принципиально они не отличаются от алгоритмов обхода деревьев.
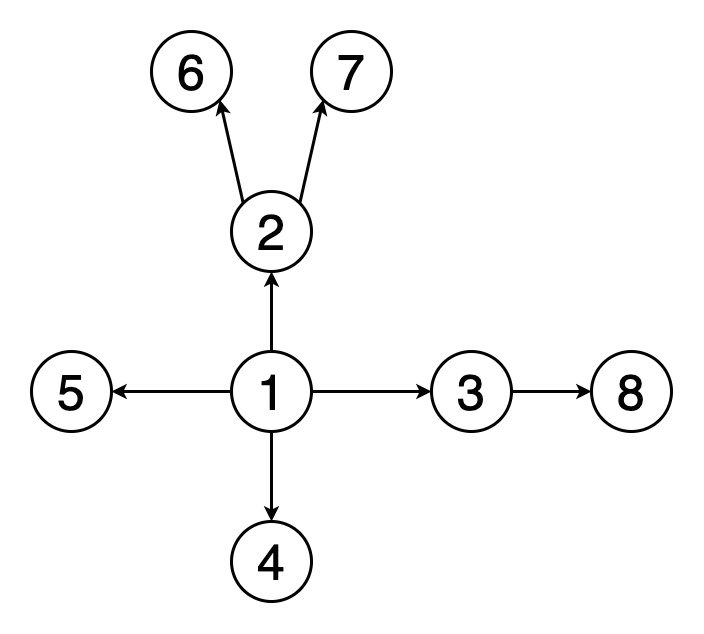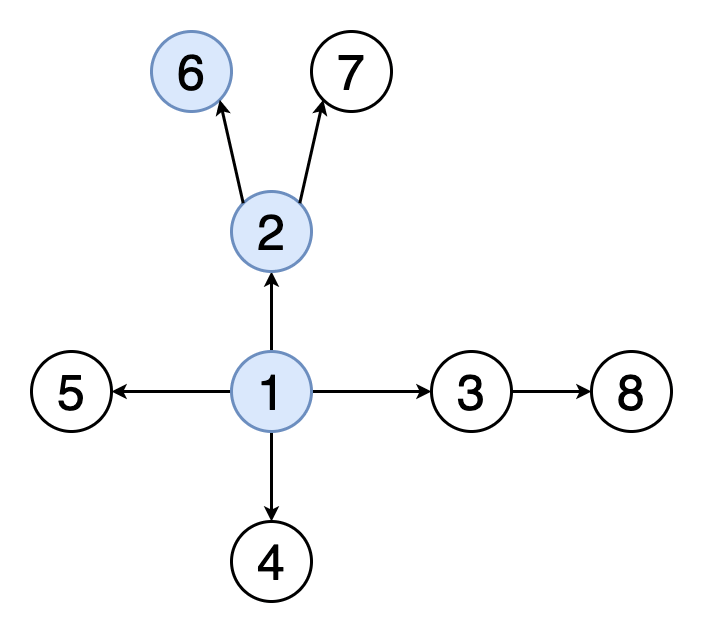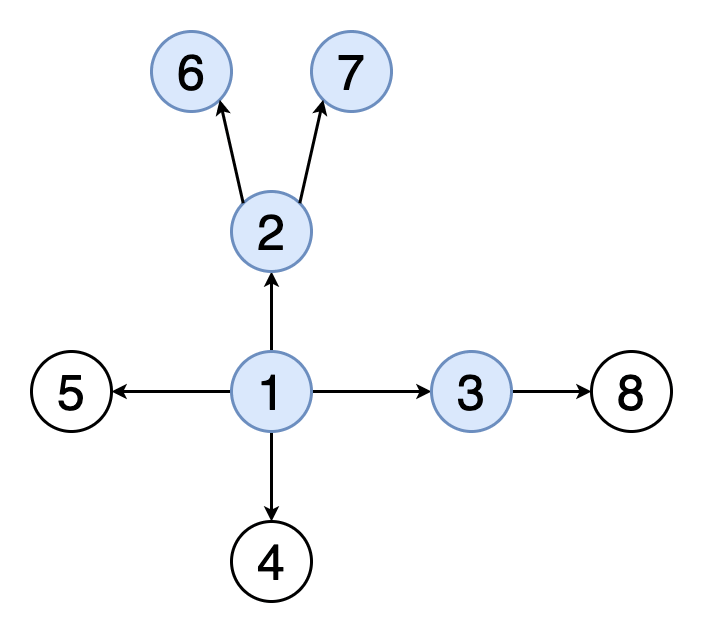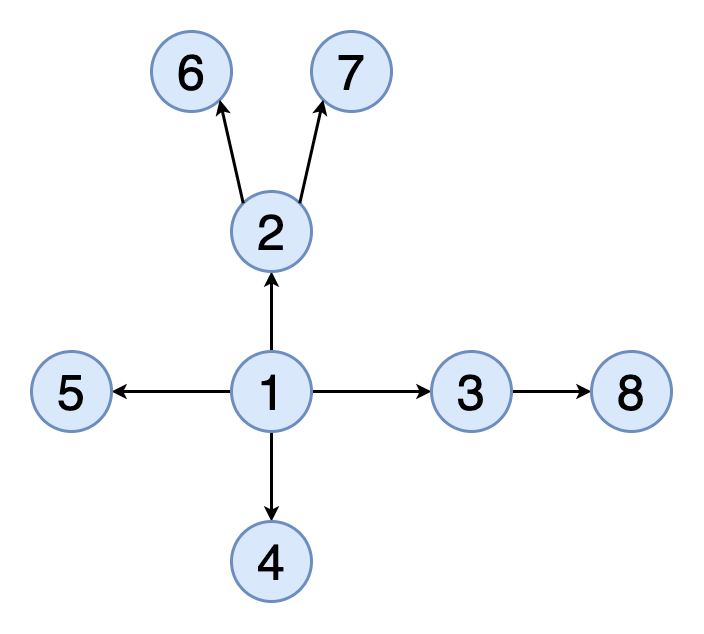
Создадим тестовый граф для демонстрации работы алгоритмов:
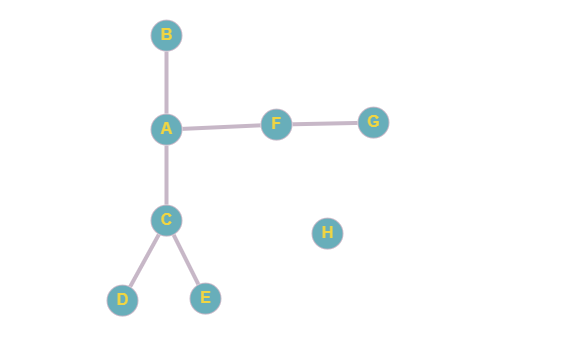
Перенесем его представление в JavaScript:
const graph = new Graph();
graph.addVertex('A');
graph.addVertex('B');
graph.addVertex('C');
graph.addVertex('D');
graph.addVertex('E');
graph.addVertex('F');
graph.addVertex('G');
graph.addVertex('H');
graph.addEdge('A', 'B');
graph.addEdge('A', 'C');
graph.addEdge('C', 'D');
graph.addEdge('C', 'E');
graph.addEdge('A', 'F');
graph.addEdge('F', 'G');
Поиск в глубину (depth-first search)
Алгоритм поиска в глубину движется последовательно по ветвям графа от начала до конца.
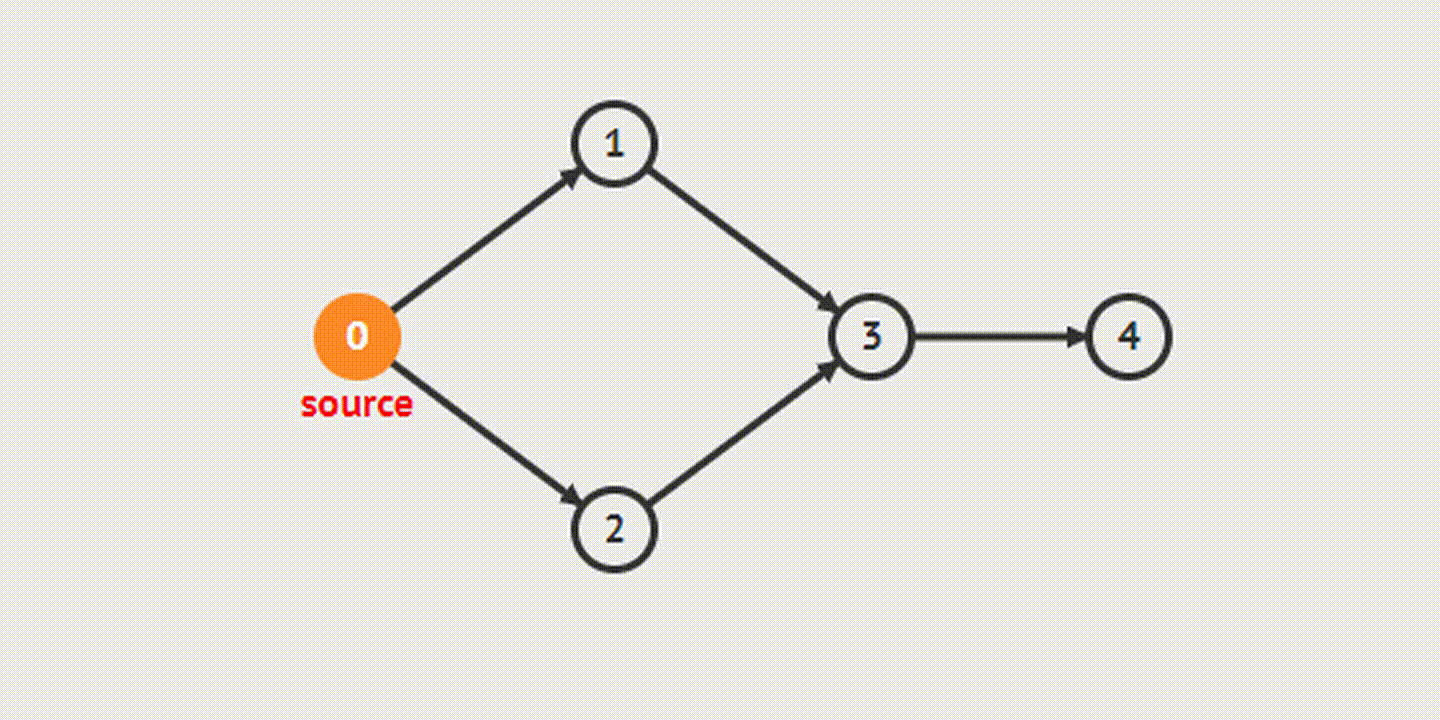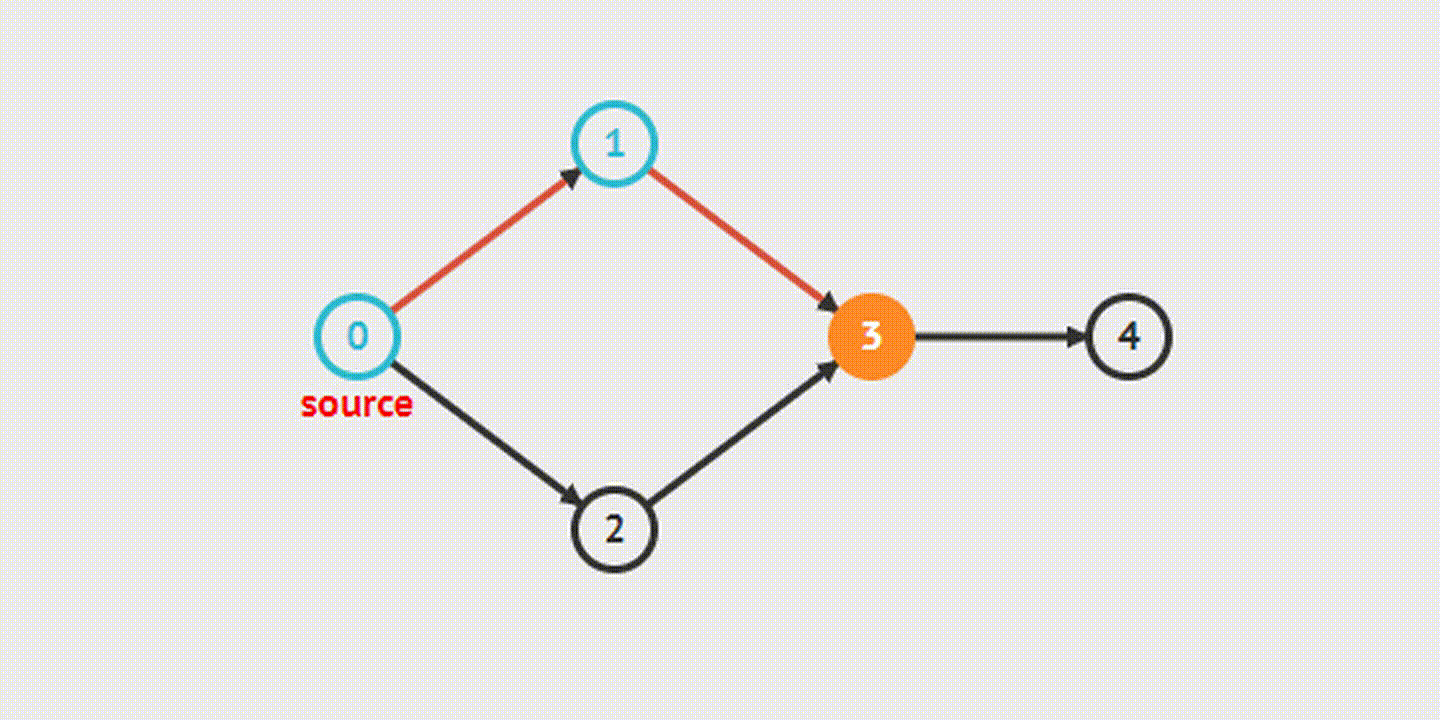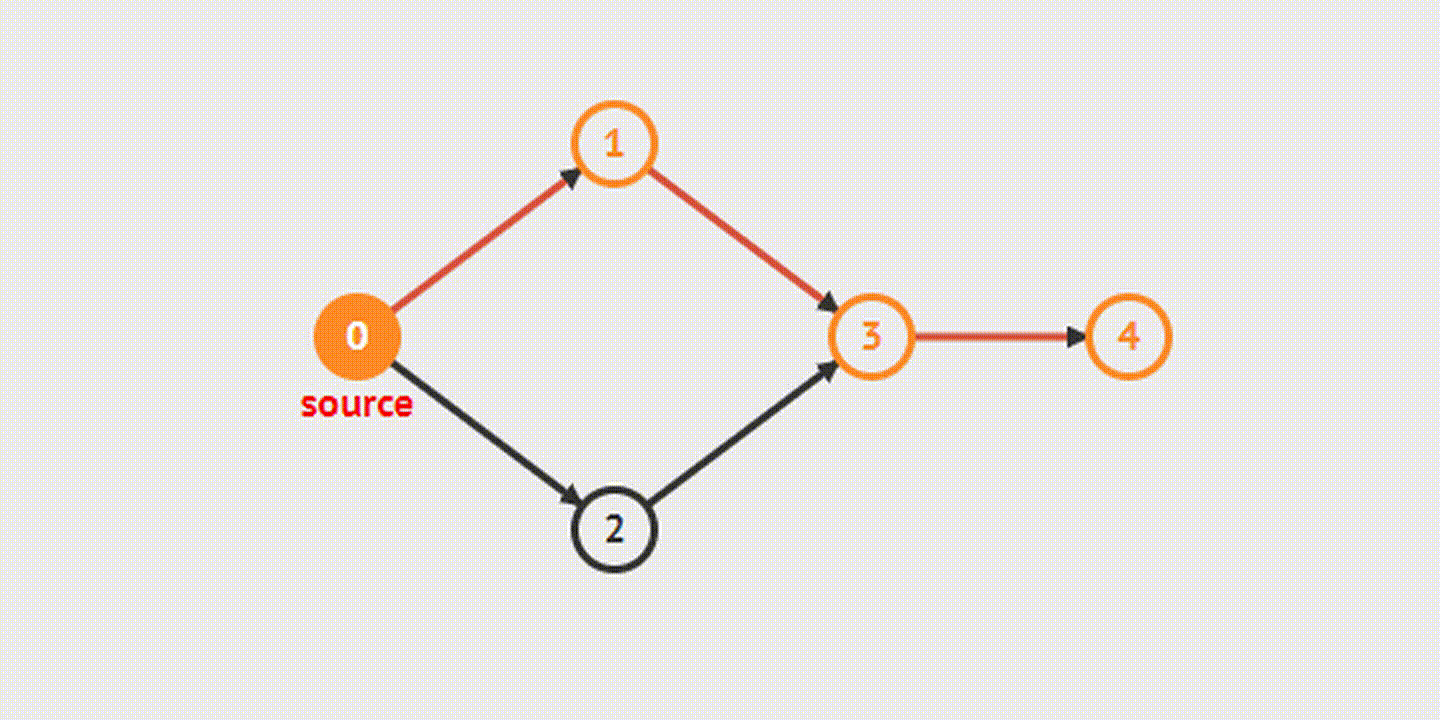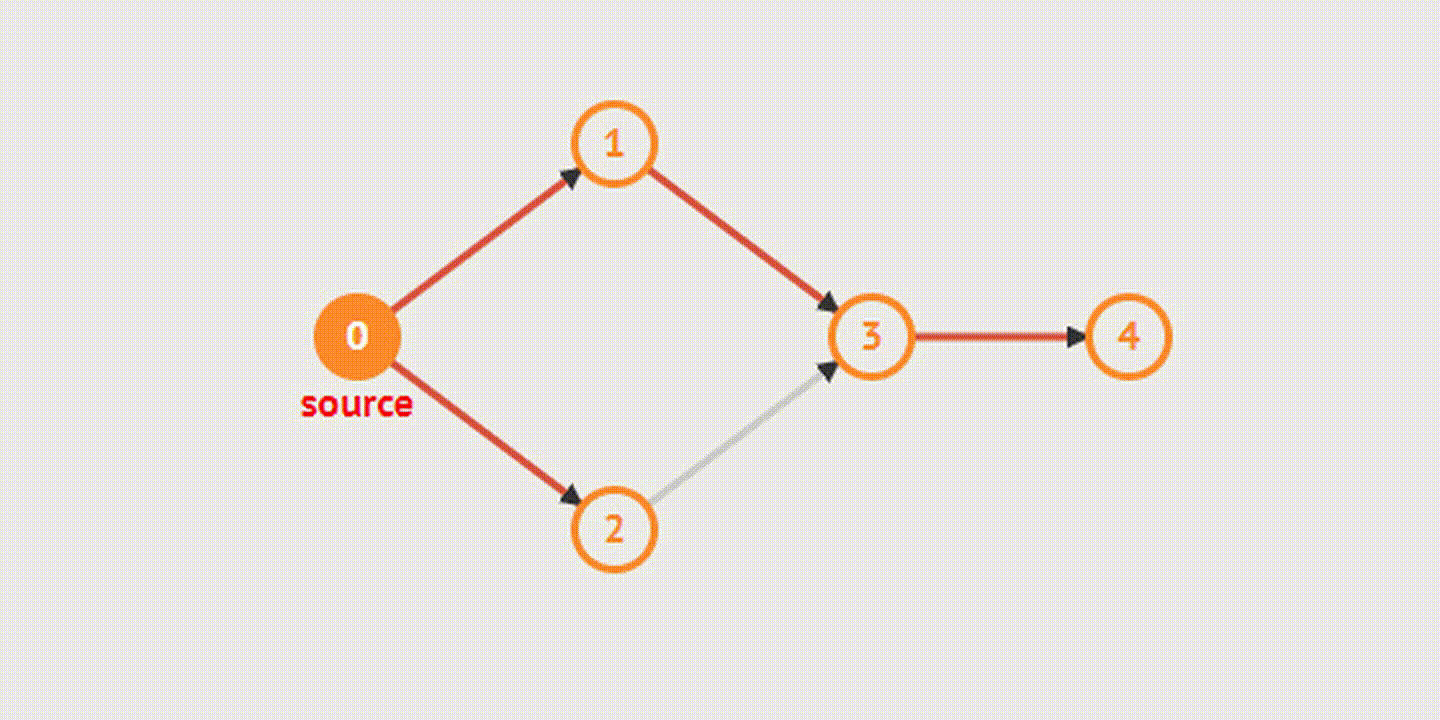
Когда мы разбирали этот алгоритм на примере деревьев, то использовали его рекурсивную реализацию – функция поиска для одного узла вызывала сама себя для его дочерних узлов. Это, вероятно, более очевидный и понятный путь, но он может приводить к переполнению стека вызовов для больших графов. Поэтому сейчас для разнообразия мы рассмотрим итеративную реализацию поиска в глубину.
Кроме того, нужно отмечать вершины, которые уже были посещены, чтобы не перебирать их повторно. В дереве нам не требовалось делать это, но графы имеют более сложную структуру, в которой могут встречаться циклы.
Перебор может начинаться с любой вершины графа. Стартовую вершину сразу же отмечаем как посещенную и добавляем ее в стек, а дальше начинается собственно алгоритм:
- Берем вершину с конца стека. В соответствии с описанием структуры данных стек это будет вершина, добавленная в него последней.
- Получаем все ее смежные вершины.
- Отбрасываем те вершины, которые уже были посещены ранее.
- Остальные отмечаем как посещенные, добавляем в стек и возвращаемся к пункту 1.
Таким образом мы будем двигаться в глубину ветки, обрабатывая сначала "более глубокие" вершины, а когда в ней закончатся непосещенные вершины, просто перейдем к следующей ветке.
На JavaScript это может выглядеть так:
class Graph {
// ..
dfs(startVertex, callback) {
let list = this.vertices; // список смежности
let stack = [startVertex]; // стек вершин для перебора
let visited = { [startVertex]: 1 }; // посещенные вершины
function handleVertex(vertex) {
// вызываем коллбэк для посещенной вершины
callback(vertex);
// получаем список смежных вершин
let reversedNeighboursList = [...list[vertex]].reverse();
reversedNeighboursList.forEach(neighbour => {
if (!visited[neighbour]) {
// отмечаем вершину как посещенную
visited[neighbour] = 1;
// добавляем в стек
stack.push(neighbour);
}
});
}
// перебираем вершины из стека, пока он не опустеет
while(stack.length) {
let activeVertex = stack.pop();
handleVertex(activeVertex);
}
// проверка на изолированные фрагменты
stack = Object.keys(this.vertices);
while(stack.length) {
let activeVertex = stack.pop();
if (!visited[activeVertex]) {
visited[activeVertex] = 1;
handleVertex(activeVertex);
}
}
}
}
Несколько важных моментов:
- Для хранения посещенных вершин мы используем не массив, а объект, так как наличие свойства в объекте проверить проще, чем наличие элемента в массиве.
- При добавлении смежных вершин в стек, мы используем метод
reverse, то есть добавляем их в обратном порядке. Это нужно для того, чтобы перебор веток происходил в том же порядке, в котором они были добавлены. - После того, как стек опустел, мы дополнительно проверяем все вершины графа на предмет посещенности. Это необходимо, так как в графе могут быть изолированные вершины или подграфы, например, в нашем тестовом графе такая вершина есть. Непосещенные вершины обрабатываем. Если в графе нет изолированных фрагментов, то эту часть можно опустить.
Запустим этот метод для нашего тестового графа:
graph.dfs('A', v => console.log(v));
Порядок перебора вершин:
A -> B -> C -> D -> E -> F -> G -> H
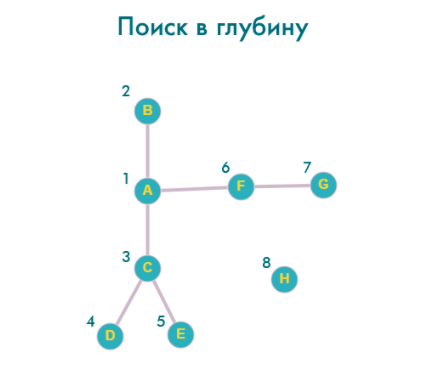
Поиск в глубину напоминает поиск пути в лабиринте, алгоритм идет по ветке, пока не упрется в "стену", после этого он возвращается назад.
Поиск в ширину (breadth-first-search)
Алгоритм поиска в ширину сначала перебирает все смежные вершины, затем смежные вершины смежных вершин и так далее по уровням.
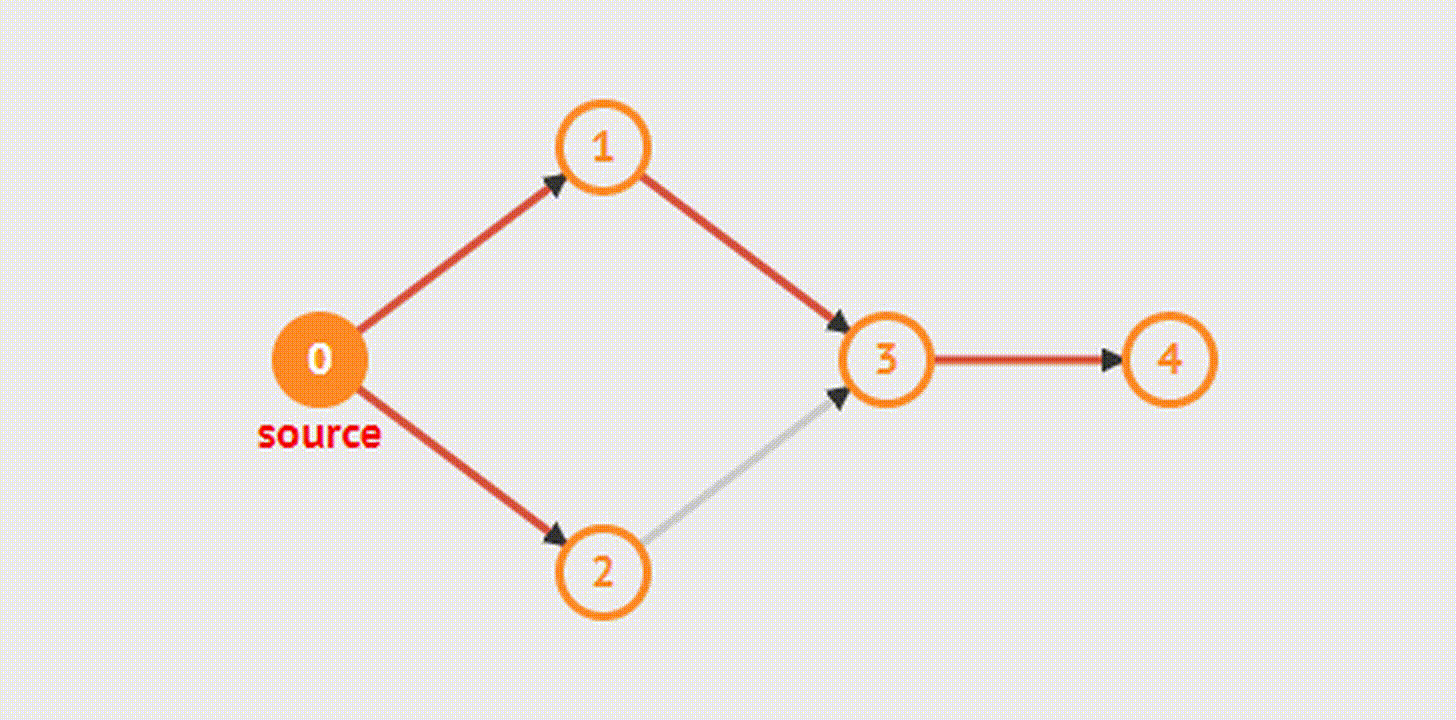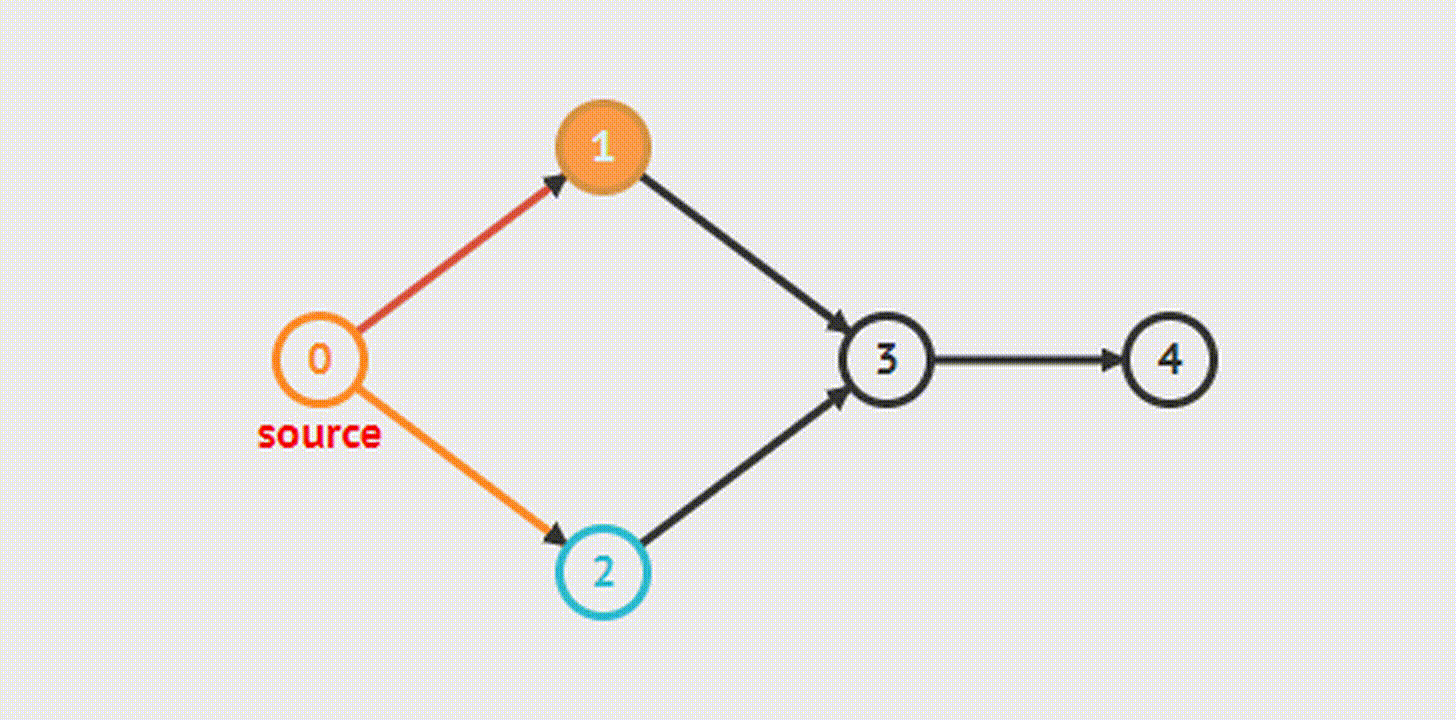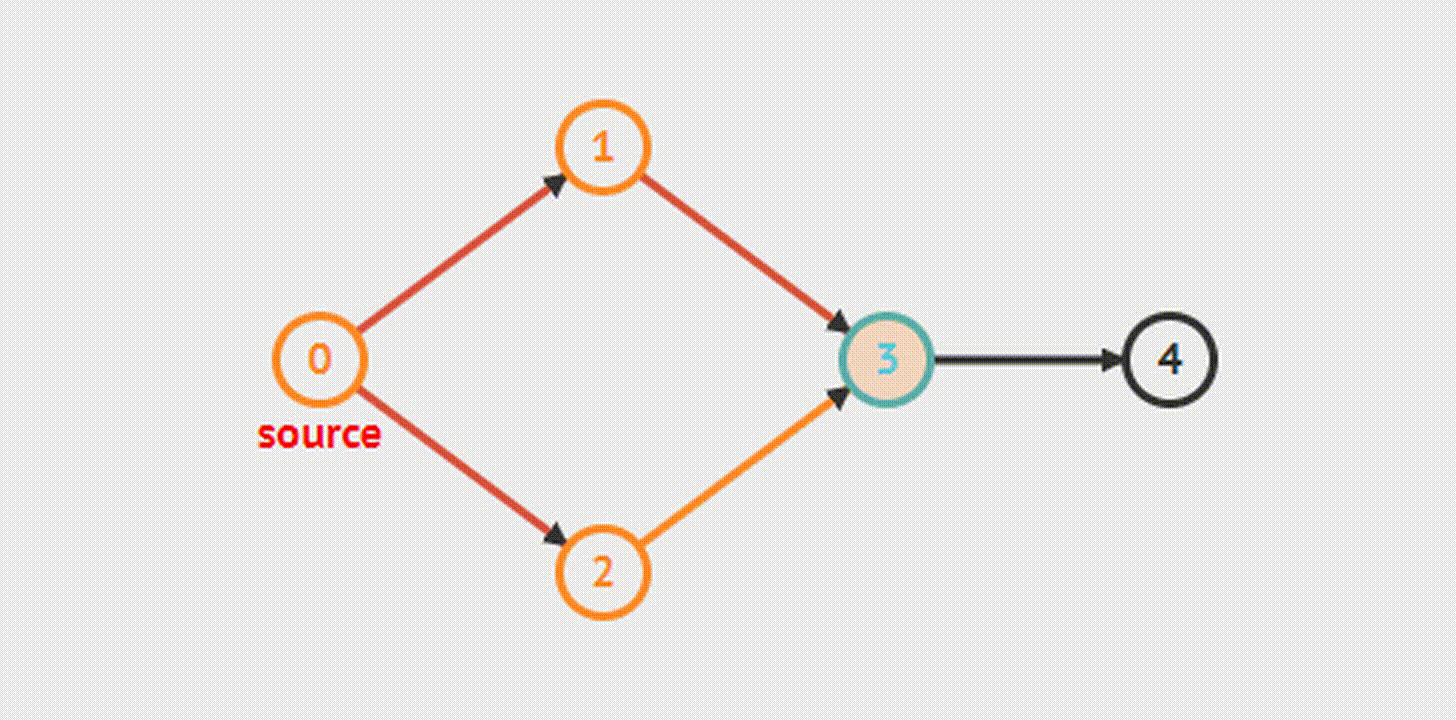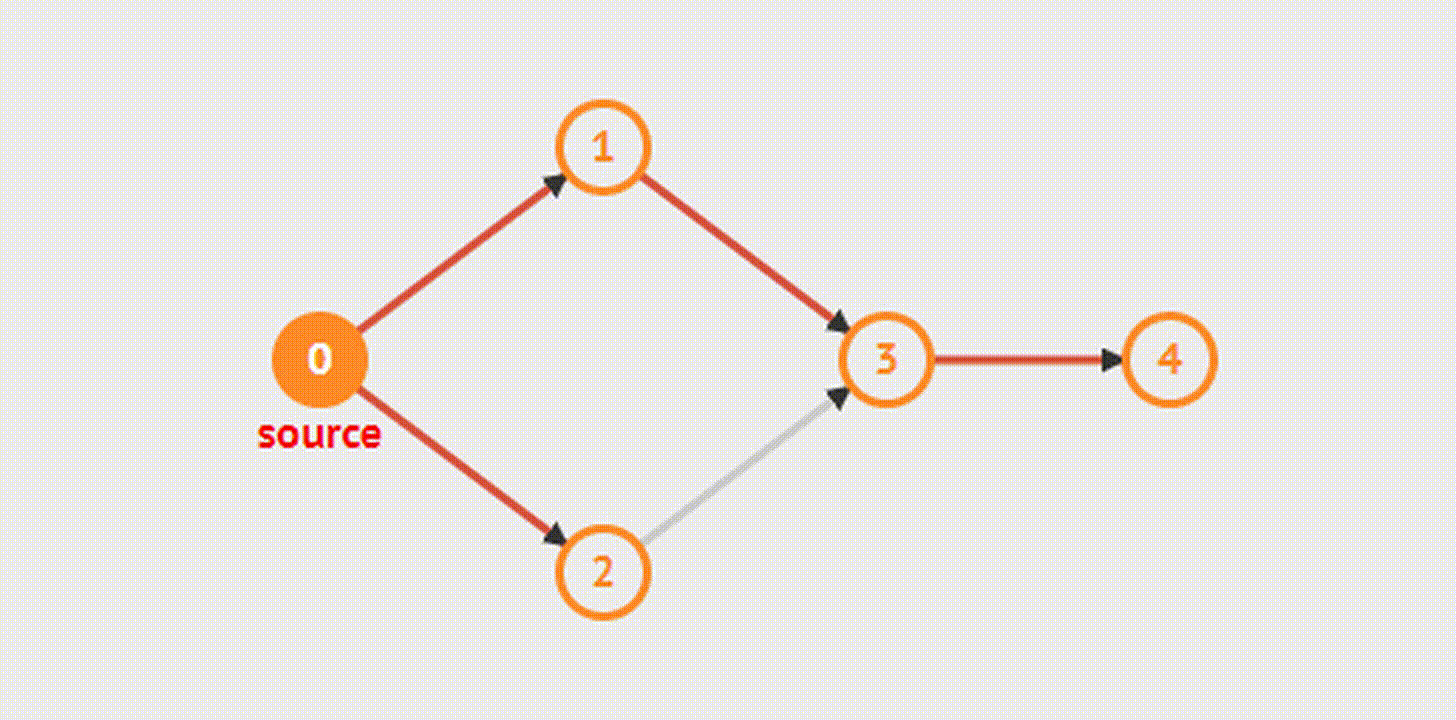
Первый узел, в которого начинается обход, отмечается как посещенный и помещается в очередь. Далее совершаем следующие действия:
- Берем вершину с начала очереди. В соответствии с описанием структуры данных очередь это будет вершина, добавленная в нее самой первой.
- Получаем все ее смежные вершины.
- Отбрасываем те вершины, которые уже были посещены ранее.
- Остальные отмечаем как посещенные, добавляем в стек и возвращаемся к пункту 1.
Обратите внимание, алгоритм абсолютно такой же, как и алгоритм поиска в глубину – разница только в порядке извлечения узлов. Вот так выбор простейшей структуры данных (стека или очереди) влияет на результат выполнения задачи.
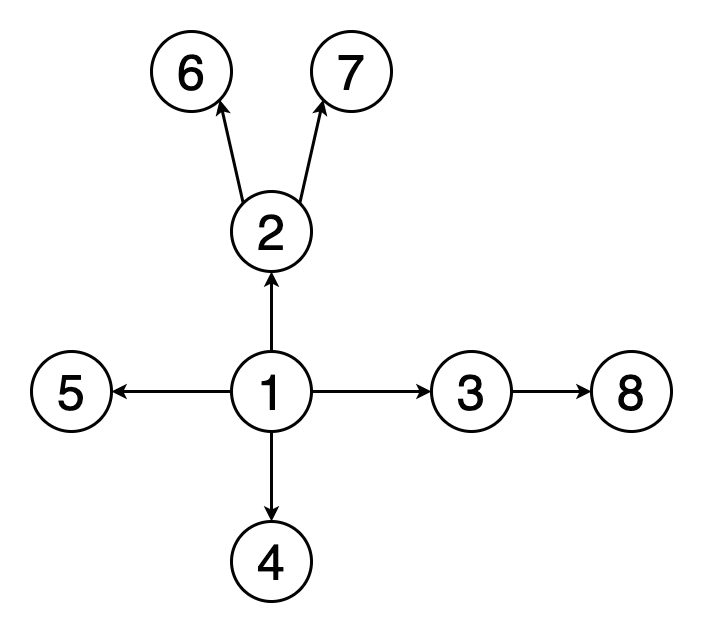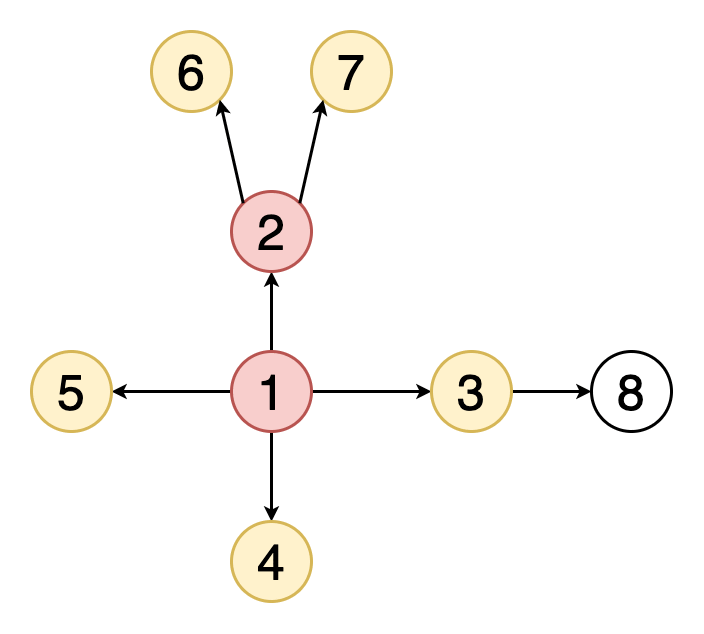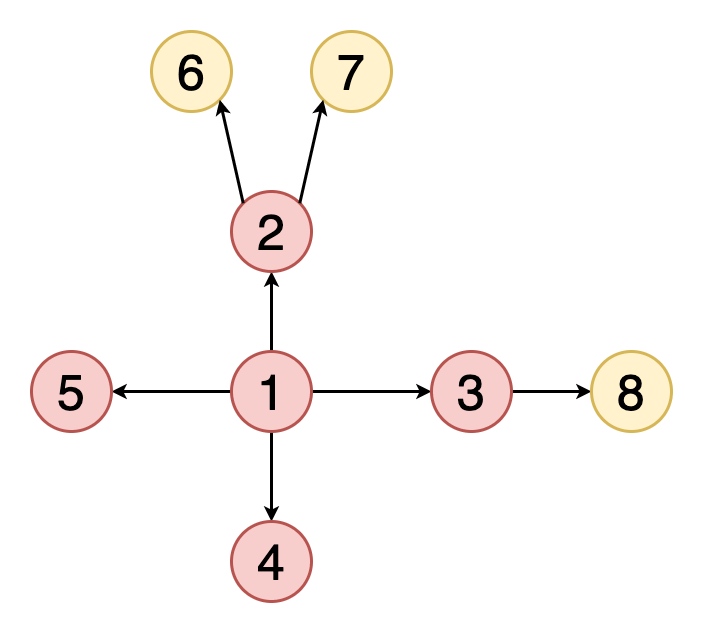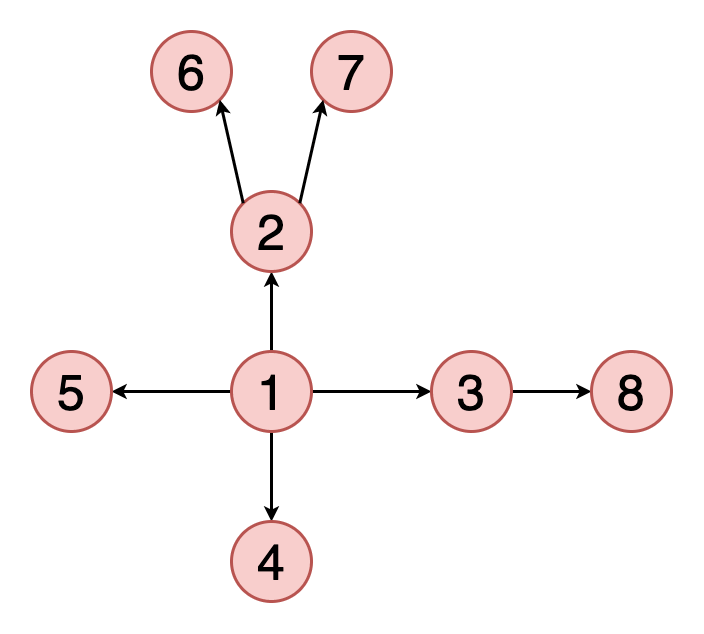
На JavaScript поиск в ширину выглядит примерно так:
class Graph {
// ..
bfs(startVertex, callback) {
let list = this.vertices; // список смежности
let queue = [startVertex]; // очередь вершин для перебора
let visited = { [startVertex]: 1 }; // посещенные вершины
function handleVertex(vertex) {
// вызываем коллбэк для посещенной вершины
callback(vertex);
// получаем список смежных вершин
let neighboursList = list[vertex];
neighboursList.forEach(neighbour => {
if (!visited[neighbour]) {
visited[neighbour] = 1;
queue.push(neighbour);
}
});
}
// перебираем вершины из очереди, пока она не опустеет
while(queue.length) {
let activeVertex = queue.shift();
handleVertex(activeVertex);
}
queue = Object.keys(this.vertices);
// Повторяем цикл для незатронутых вершин
while(queue.length) {
let activeVertex = queue.shift();
if (!visited[activeVertex]) {
visited[activeVertex] = 1;
handleVertex(activeVertex);
}
}
}
}
В этой реализации мы не переворачиваем массив смежных вершин, так как из очереди они и так будут извлекаться в правильном порядке.
После перебора основного дерева обязательно повторяем процедуру для всех изолированных вершин.
Запустим этот метод для нашего тестового графа:
graph.bfs('A', v => console.log(v));
Порядок перебора вершин:
A -> B -> C -> F -> D -> E -> G -> H
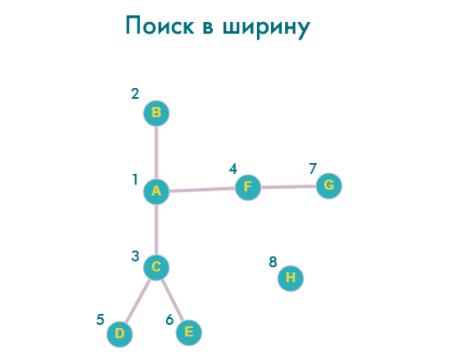
Рисунок поиска в ширину напоминает круги на воде – сначала исследуются вершины в границах маленького круга, затем он увеличивается.
Поиск кратчайшего пути
Одной из базовых задач при работе с графами является определение кратчайшего пути между двумя вершинами. Такие алгоритмы очень востребованы, например, в картографических сервисах (Google maps) для прокладывания маршрута между двумя точками.
Вариантов постановки этой задачи очень много, мы начнем с самого простого.
Представьте, что вам требуется построить маршрут, проходящий через наименьшее количество станций или населенных пунктов.
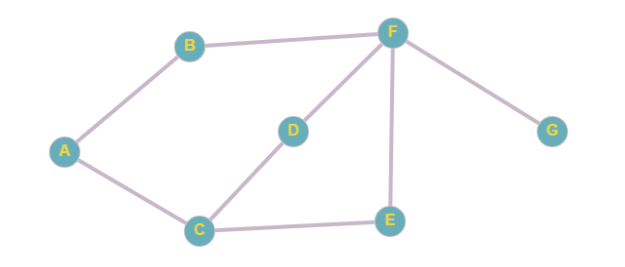
Например, в этом графе из точки A в точку G можно попасть тремя разными способами. Как выяснить, какой из них самый быстрый?
Сначала создадим JavaScript-представление этой структуры:
let graph = new Graph();
graph.addVertex('A');
graph.addVertex('B');
graph.addVertex('C');
graph.addVertex('D');
graph.addVertex('E');
graph.addVertex('F');
graph.addVertex('G');
graph.addVertex('H');
graph.addEdge('A', 'B');
graph.addEdge('B', 'F');
graph.addEdge('F', 'G');
graph.addEdge('A', 'C');
graph.addEdge('C', 'D');
graph.addEdge('D', 'F');
graph.addEdge('C', 'E');
graph.addEdge('E', 'F');
Для решения нашей задачи подойдет уже знакомый нам алгоритм поиска в ширину с некоторыми модификациями.
Необходимо по ходу работы алгоритма сохранять дополнительную информацию, чтобы затем восстановить путь из исходной вершины в искомую. Мы будем сохранять расстояние каждой вершины от исходной, а также для каждой вершины – предыдущую вершину, из которой мы пришли.
class Graph {
// ..
bfs2(startVertex) {
let list = this.vertices;
let queue = [startVertex];
let visited = { [startVertex]: 1 };
// кратчайшее расстояние от стартовой вершины
let distance = { [startVertex]: 0 };
// предыдущая вершина в цепочке
let previous = { [startVertex]: null };
function handleVertex(vertex) {
let neighboursList = list[vertex];
neighboursList.forEach(neighbour => {
if (!visited[neighbour]) {
visited[neighbour] = 1;
queue.push(neighbour);
// сохраняем предыдущую вершину
previous[neighbour] = vertex;
// сохраняем расстояние
distance[neighbour] = distance[vertex] + 1;
}
});
}
// перебираем вершины из очереди, пока она не опустеет
while(queue.length) {
let activeVertex = queue.shift();
handleVertex(activeVertex);
}
return { distance, previous }
}
}
Обработка изолированных фрагментов графа здесь не требуется. Между изолированными подграфами пути нет, ни кратчайшего, ни какого-либо другого, мы и так это увидим.
Опробуем обновленный алгоритм:
let data = graph.bfs2('A');
/*
{
distance: {
A: 0,
B: 1,
C: 1,
D: 2,
E: 2,
F: 2,
G: 3
},
previous: {
A: null,
B:'A',
C:'A',
D:'C',
E: 'C',
F:'B',
G: 'F'
},
}
*/
В свойстве distance хранятся кратчайшие расстояния от вершины А до всех остальных вершин графа. Выходит, что до вершины G можно добраться всего за три шага. А восстановить этот путь поможет свойство previous, которое хранит всю цепочку шагов:
class Graph {
// ...
findShortestPath(startVertex, finishVertex) {
let result = this.bfs2(startVertex);
if (!(finishVertex in result.previous))
throw new Error(`Нет пути из вершины ${startVertex} в вершину ${finishVertex}`);
let path = [];
let currentVertex = finishVertex;
while(currentVertex !== startVertex) {
path.unshift(currentVertex);
currentVertex = result.previous[currentVertex];
}
path.unshift(startVertex);
return path;
}
}
Запустим алгоритм поиска:
graph.findShortestPath('A', 'G'); // ['A', 'B', 'F', 'G']
graph.findShortestPath('A', 'Z'); // Error: Нет пути из вершины A в вершину Z
Взвешенные графы
Зачастую нам интересен не только факт наличия связи между двумя сущностями (смежность вершин, наличие ребра между ними), но и некоторые характеристики этой связи.
Для примера возьмем карту метро. Перегоны между станциями отличаются расстоянием.
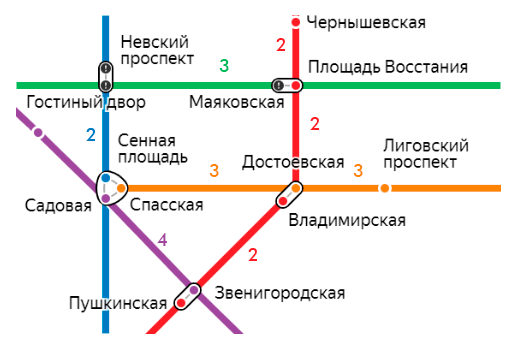
В этом графе каждому ребру (перегон) соответствует число, равное времени в пути в минутах между смежными станциями. Это число называют весом ребра, а сам граф взвешенным.
Представление взвешенного графа
Для взвешенного графа необходимо хранить не только факт связи, но и вес ребра, соединяющего две вершины.
Попробуем перенести в JavaScript вот такой граф:
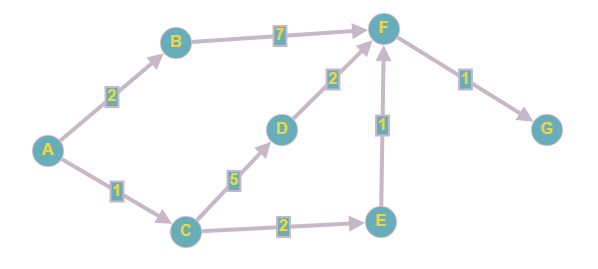
Если мы используем матрицу смежности, то веса можно подставлять вместо единиц и нулей (наличие или отсутствие связи).
| A | B | C | D | E | F | G | |
| A | 0 | 2 | 1 | 0 | 0 | 0 | 0 |
| B | 0 | 0 | 0 | 0 | 0 | 7 | 0 |
| C | 0 | 0 | 0 | 5 | 2 | 0 | 0 |
| D | 0 | 0 | 0 | 0 | 0 | 2 | 0 |
| E | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| F | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| G | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
В списках смежности нужно поставить в соответствие каждой смежной вершине вес ребра, ведущего к ней. Для этого мы можем использовать, например, вложенные массивы:
let graph = {
a: [ [b, 2], [c, 1] ],
b: [ [f, 7] ],
c: [ [d, 5], [e, 2] ],
d: [ [f, 2] ],
e: [ [f, 1] ],
f: [ [g, 1] ],
g: [ ]
}
Первым элементом в массиве идет сама смежная вершина, вторым – длина пути до нее (вес ребра).
Или можно представить то же самое с помощью объектов JavaScript:
let graph = {
a: { b: 2, c: 1 },
b: { f: 7 },
c: { d: 5, e: 2 },
d: { f: 2 },
e: { f: 1 },
f: { g: 1 },
g: { },
}
Дальше мы будем использовать именно такое представление.
Кратчайший путь во взвешенном графе
Задача поиска кратчайшего пути во взвешенном графе встречается еще чаще, чем в невзвешенном. Например, для построения самого быстрого маршрута между двумя станциями метро или для сетевых протоколов маршрутизации. И здесь все намного интереснее. Мы не можем полагаться на количество ребер между вершинами, а значит, поиск в ширину нам не поможет.
Для поиска кратчайшего пути во взвешенных графах существует множество алгоритмов. Некоторые из них могут работать даже с отрицательными весами. Мы рассмотрим один из самых популярных.
Алгоритм Дейкстры
Он похож на поиск в ширину – мы начинаем со стартовой вершины и перебираем ее смежные вершины. На каждом шаге мы рассчитываем все возможные пути до вершины и выбираем среди них самый короткий.
Изначально полагается, что путь до каждой вершины неизвестен и равен бесконечности, кроме пути до стартовой вершины, который равен нулю.
На каждом шаге выбирается самая близкая из известных вершин. На первом шаге это стартовая вершина, так как о других мы просто ничего не знаем.
Для выбранной вершины мы можем получить ее смежные вершины и расстояния до них (вес ребер). А зная расстояние от стартовой вершины до текущей и расстояния от текущей вершины до ее смежных вершин, мы можем рассчитать и расстояния от стартовой вершины до смежных.
Текущая вершина отмечается как посещенная и в дальнейших манипуляциях не участвует.
Затем все действия повторяются: мы выбираем самую близкую из известных вершин, не считая посещенных. Теперь известных вершин стало больше, поэтому есть из чего выбирать. Находим смежные вершины и обновляем расстояния до них.
Если расстояние для какой-то вершины уже было определено на предыдущих шагах, мы должны сравнить его с новым и выбрать минимальное.
Чтобы восстановить кратчайший путь до нужной вершины, мы дополнительно должны сохранять предыдущую вершину в этом пути, как мы уже делали для невзвешенного графа.
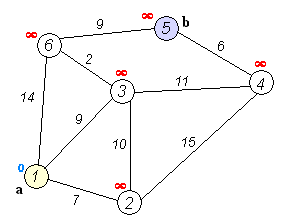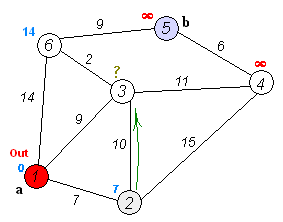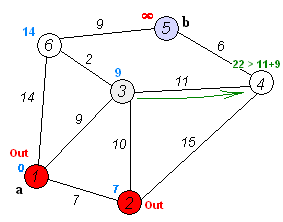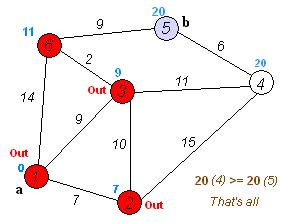
Реализация алгоритма Дейкстры на JavaScript
Для реализации алгоритма Дейкстры на потребуется вспомогательная функция для поиска ближайшей вершины из известных:
function findNearestVertex(distances, visited) {
let minDistance = Infinity;
let nearestVertex = null;
Object.keys(distances).forEach(vertex => {
if (!visited[vertex] && distances[vertex] < minDistance) {
minDistance = distances[vertex];
nearestVertex = vertex;
}
});
return nearestVertex;
}
Она принимает объект distances, в котором каждой вершине соответствует известное на данный момент расстояние, и объект visited, в котором отмечены посещенные вершины.
Сам алгоритм выглядит так:
function dijkstra(graph, startVertex) {
let visited = {};
let distances = {}; // кратчайшие пути из стартовой вершины
let previous = {}; // предыдущие вершины
let vertices = Object.keys(graph); // список вершин графа
// по умолчанию все расстояния неизвестны (бесконечны)
vertices.forEach(vertex => {
distances[vertex] = Infinity;
previous[vertex] = null;
});
// расстояние до стартовой вершины равно 0
distances[startVertex] = 0;
function handleVertex(vertex) {
// расстояние до вершины
let activeVertexDistance = distances[vertex];
// смежные вершины (с расстоянием до них)
let neighbours = graph[activeVertex];
// для всех смежных вершин пересчитать расстояния
Object.keys(neighbours).forEach(neighbourVertex => {
// известное на данный момент расстояние
let currentNeighbourDistance = distances[neighbourVertex];
// вычисленное расстояние
let newNeighbourDistance = activeVertexDistance + neighbours[neighbourVertex];
if (newNeighbourDistance < currentNeighbourDistance) {
distances[neighbourVertex] = newNeighbourDistance;
previous[neighbourVertex] = vertex;
}
});
// пометить вершину как посещенную
visited[vertex] = 1;
}
// ищем самую близкую вершину из необработанных
let activeVertex = findNearestVertex(distances, visited);
// продолжаем цикл, пока остаются необработанные вершины
while(activeVertex) {
handleVertex(activeVertex);
activeVertex = findNearestVertex(distances, visited);
}
return { distances, previous };
}
Запустим алгоритм для нашего взвешенного графа:
dijkstra(graph, 'a');
/*
{
distances: {
a: 0,
b: 2,
c: 1,
d: 6,
e: 3,
f: 4,
g: 5
},
previuos: {
a: null,
b: 'a',
c: 'a',
d: 'c',
e: 'c',
f: 'e',
g: 'f',
}
}
*/
Кратчайший путь от A до G составляет 5 и проходит через вершины ACEFG (Алгоритм восстановления пути по объекту previous рассмотрен выше).
Заключение
В современном информационном мире графы – одна из важнейших структур данных, которая позволяет отобразить связи между объектами. Одновременно это одна из самых сложных структур. Существует множество разновидностей графов: кроме взвешенных и ориентированных графов, с которыми мы познакомились, существуют, например, псевдографы (графы, в структуре которых содержатся петли). Соответственно, существует и множество алгоритмов, работающих с графами.
Мы разобрали практически все популярные структуры данных, которые могут пригодиться JavaScript-разработчику в работе или на собеседовании: массивы, связные списки, стеки и очереди, а также деревья и графы.
В следующей статье цикла мы поговорим про еще одну очень важную структуру – хеш-таблицу.





Комментарии