Если хочешь подтянуть свои знания, загляни на наш курс «Алгоритмы и структуры данных», на котором ты:
- углубишься в решение практических задач;
- узнаешь все про сложные алгоритмы, сортировки, сжатие данных и многое другое.
Ты также будешь на связи с преподавателем и другими студентами.
В итоге будешь браться за сложные проекты и повысишь чек за свою работу 🙂
В предыдущих статьях серии мы разобрали все основные структуры данных и алгоритмы для работы с ними, а также их особенности в JavaScript.
Другие статьи цикла:
- Часть 1. Основные понятия и работа с массивами
- Часть 2. Стеки, очереди и связные списки
- Часть 3. Деревья
- Часть 4. Графы
- Часть 5. Объекты и хеширование
Битовое представление чисел
JavaScript поддерживает возможность побитовых манипуляций с числами. Это довольно низкий уровень абстракции, к которому мы редко обращаемся в веб-разработке, но иметь общее представление о нем полезно.
Двоичная система счисления
Любое число может быть переведено в двоичную систему счисления и представлено как последовательность из 32 битов (единиц и нулей).
| Десятичная | Двоичная | Двоичная, 32 бита |
| 1 | 1 | 00000000000000000000000000000001 |
| 2 | 10 | 00000000000000000000000000000010 |
| 5 | 101 | 00000000000000000000000000000101 |
| 10 | 1010 | 00000000000000000000000000001010 |
Чтобы перевести число в двоичную систему, можно воспользоваться любым онлайн-сервисом или нативным методом языка toString:
let number = 5;
number.toString(2); // '101'
Для обратного перевода двоичных чисел в десятичную систему можно использовать функцию parseInt с указанием основания системы:
let bNumber = '101';
parseInt(bNumber, 2); // 5
Отрицательные числа
Для битового представления отрицательных чисел используется специальный формат – дополнение до двойки. Сначала в двоичную систему переводится абсолютная величина (модуль) числа, затем каждый бит результата изменяется на противоположный, и наконец к полученному числу прибавляется единица.
Итак, чтобы получить битовое представление числа -10, нужно:
1) Получить битовое представление модуля числа (10):
00000000000000000000000000001010
2) Обратить каждый бит:
11111111111111111111111111110101
3) Прибавить единицу:
11111111111111111111111111110110
Благодаря такому алгоритму мы можем быстро определить, какое число перед нами. Если первый (старший) бит равен 0, значит, число положительное, если 1, то отрицательное. Поэтому первый бит называется знаковым.
Побитовые операторы
Они практически ничем не отличаются от логических операторов, даже символы у них похожие.
Бинарные операторы
Бинарные операторы побитового И (&), побитового ИЛИ (|) и исключающего ИЛИ (^) принимают два числовых операнда (в десятичной системе счисления), каждый из которых переводится в 32-битную последовательность. Затем соответствующая логическая операция производится поочередно с каждой парой бит. Полученный результат переводится обратно в десятичную систему счисления.
Например, побитовое сложение чисел 5 и 6 выглядит так:
5 | 6
1) Привести оба операнда к битовому представлению:
5 => 00000000000000000000000000000101
6 => 00000000000000000000000000000110
2) Произвести операцию логического ИЛИ для каждой пары битов:
00000000000000000000000000000111
3) Перевести полученный результат в десятичную систему:
00000000000000000000000000000111 => 7
Таким образом, 5 | 6 = 7.
Побитовое НЕ
В JavaScript также есть унарный оператор побитового НЕ (~), который просто заменяет каждый бит числа на противоположный. Ожидаемо, для положительных чисел результатом будет отрицательное число и наоборот.
~10 => -11
~(-11) => 10
Битовый сдвиг
Больше всего трудностей обычно вызывают операторы побитового сдвига:
- левый сдвиг (
<<), - правый сдвиг (
>>) - правый сдвиг с заполнением нулями (
>>>).
Рассмотрим для примера сдвиг числа 10 на 2 бита вправо (правый сдвиг числа 10 на два бита):
10 >> 2
1) Вычисляем двоичное представление числа 10:
00000000000000000000000000001010
2) Отбрасываем два правых бита:
000000000000000000000000000010
3) Теперь необходимо дополнить полученный результат до 32 битов. При обычном правом сдвиге для этого копируется старший бит нужное количество раз. Это позволяет сохранить знак числа. Существует также оператор правого сдвига с заполнением нулями (>>>):
00000000000000000000000000000010 => 2
В итоге получается, что 10 >> 2 => 2.
Использование
Побитовые операции в JavaScript используются крайне редко, в основном для более короткой записи некоторых выражений.
Проверка на четность
Число 1 в двоичном представлении выглядит так:
00000000000000000000000000000001
У всех четных чисел последний (младший) бит равен 0. Если мы побитово умножим любое четное число на единицу, то получим 0. На этом может быть основана проверка числа на четность:
function isEven(number) {
return (number & 1) === 0;
}
Умножение и деление на степени двойки
Операция битового сдвига влево сдвигает двоичное число на несколько разрядов, то есть по сути умножает его на двойку в некоторой степени:
5 << 3 === 5 * Math.pow(2, 3)
Округление вниз
Побитовые операторы работают только с целой частью числа, отбрасывая дробную, поэтому их можно использовать для округления. Но для этого подойдет не каждая побитовая операция – важно чтобы она не изменяла значение числа:
// двойное побитовое НЕ
~~4.345 // 4
// побитовое ИЛИ с нулем
4.345 ^ 0 // 4
Используя побитовые операторы всегда следует помнить о читаемости кода. Если не все члены вашей команды с ними на ты, лучше ими не злоупотреблять.
Множества
Множество – это неупорядоченная совокупность каких-либо объектов – элементов множества. Например, множество пользователей вашего сайта или множество товаров вашего интернет-магазина.
has (проверка наличия элемента по значению) и delete (удаление элемента по значению).Основные алгоритмы для работы с множествами:
- объединение двух множеств в новое большое множество;
- пересечение двух множеств – определение элементов, которые входят в оба множества;
- разность двух множеств – определение элементов, которые входят только в одно из множеств.
Реализуем их для Set.
Объединение:
function union(set1, set2) {
let result = new Set(set1);
for (let el of set2) {
result.add(el);
}
return result;
}
// или
function union2(set1, set2) {
return new Set([...set1, ...set2]);
}
Пересечение:
function intersection(set1, set2) {
let result = new Set();
for (let el of set2) {
if (set1.has(el)) result.add(el);
}
return result;
}
// или
function intersection2(set1, set2) {
return new Set([...set1].filter(el => set2.has(el)));
}
Разность:
function difference(set1, set2) {
let result = new Set(set1);
for (let el of set2) {
result.delete(el);
}
return result;
}
// или
function difference2(se1, set2) {
return new Set([...set1].filter(el => !set2.has(el)));
}
Кэширование вычислений
Кэширование – это прием оптимизации сложных вычислений, при котором однажды полученные результаты сохраняются и могут быть использованы повторно без необходимости снова выполнять само вычисление.
Рассмотрим концепцию кэширования на простом примере – вычислении факториала числа n.
function factorial(n) {
console.log('Выполняется вычисление');
let result = 1;
while(n){
result *= n--;
}
return result;
}
factorial(5); // 'Выполняется вычисление'
factorial(5); // 'Выполняется вычисление'
factorial(5); // 'Выполняется вычисление'
Мы трижды вызываем функцию с одним и тем же аргументом, и она трижды выполняет вычисление его квадрата. А ведь у нее внутри цикл, следовательно, чем больше будет число, тем дольше будет выполняться расчет.
Было бы неплохо, чтобы функция factorial умела "запоминать" результаты предыдущих вычислений. Для этого мы добавим ей кэш:
const cachedFactorial = (() => {
const cache = {};
return n => {
if (n in cache) return cache[n];
console.log('Выполняется вычисление');
let result = 1;
for (let i = n; i > 0; i--) {
result *= i;
}
cache[n] = result; // "запоминание" результата
return result;
}
})();
Кэш – это простой объект, ключами которого являются входные параметры функции, а значениями – результаты вычислений для этих параметров.
Здесь используется IIFE-синтаксис (функция, которая вызывается прямо на месте создания). Это нужно для создания замыкания, чтобы возвращенная функция всегда имела доступ к кэшу.
Теперь вычисление факториала для 5 выполняется только в первый раз, а затем используется ранее сохраненный результат.
cachedFactorial(5); // 'Выполняется вычисление'
cachedFactorial(5); // ...
cachedFactorial(5); // ...
Кэширование будет полезно не только для сложных вычислений, но и для длительных операций, например, запросов к серверу. Чтобы не загружать данные для одного и того же пользователя многократно, их можно кэшировать на клиентской стороне.
Чтобы не добавлять кэш функциям вручную, имеет смысл написать функцию-декоратор:
function addCache(fn) {
let cache = {};
return function(param) {
if (!(param in cache)) {
cache[param] = fn.call(this, param);
}
return cache[param];
};
}
const factorialWithCache = addCache(factorial);
Кэширование в динамическом программировании
Мемоизация вычислений – важная составная часть концепции динамического программирования, о которой мы уже вскользь упоминали в первой статье серии.
Динамическое программирование — это когда у нас есть задача, которую непонятно как решать, и мы разбиваем ее на меньшие задачи, которые тоже непонятно как решать. (с)
Динамическое программирование использует стратегию "разделяй и властвуй", разбивая большую задачу на более простые подзадачи, но идет еще дальше и пытается эти подзадачи оптимизировать, чтобы не совершать одно и то же действие несколько раз. Для этого как раз и используется кэш.
Есть два подхода к заполнению кэша:
- мемоизация – заполнение "сверху вниз", обычно рекурсивное;
- табуляция – заполнение "снизу вверх", обычно итеративное.
Заезженный, но очень понятный пример – последовательность Фибоначчи, в которой каждый элемент является суммой двух предыдущих элементов.
0 1 1 2 3 5 8 13 21
При этом первые элементы (0 и 1) известны.
Предположим, что у нас есть задача найти n-ное число Фибоначчи, и рассмотрим для нее обе стратегии кэширования.
Табуляция
Стратегия табуляции предусматривает пошаговое заполнение кэша снизу вверх – от младших членов последовательности к старшим.
function fibonacciTabulation(n) {
let cache = [];
cache[0] = 0;
cache[1] = 1;
for (let i = 2; i <= n; i++) {
cache[i] = cache[i - 2] + cache[i - 1];
}
return cache[n];
}
Мемоизация
Стратегия мемоизации отталкивается от формального описания проблемы и нацелена прежде всего именно на поиск решения – она более декларативная и обычно использует рекурсию.
Формальное описание проблемы: n-ный член является суммой двух предыдущих членов, то есть fib(6) = fib(5) + fib(4). Таким образом, мы разбиваем одну задачу на две задачи поменьше.
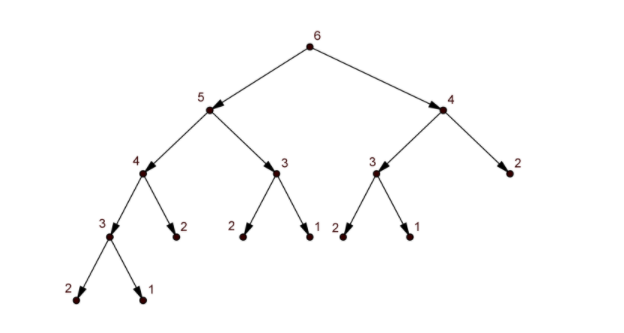
f(6) = f(5) + f(4)
f(5) = f(4) + f(3)
f(4) = f(3) + f(2)
// …
Вы наверняка уже заметили, что подзадачи в разных ветках вычислений перекрываются, то есть младшие члены последовательности будут вычисляться много раз.
Если мы будем запоминать ранее вычисленные элементы, то сможем здорово сократить дерево вычислений:
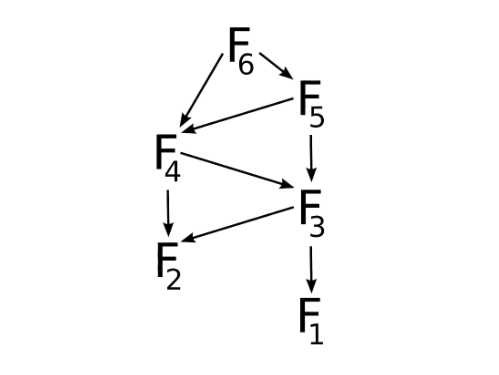
function fibonacciMemoization(n) {
let cache = {};
let recursive = (n) => {
// член последовательности уже был посчитан
if (n in cache) return cache[n];
// вычисление n-ного члена и сохранение его в кэше
let result;
if (n < 2) result = n;
else result = recursive(n-2) + recursive(n-1);
cache[n] = result;
return cache[n];
}
return recursive(n);
}
Если все возможные подзадачи решать необязательно, то мемоизация может быть полезнее, так как рекурсивное вычисление можно прервать при достижении нужного значения.
Трансформации
translate, rotate, scale и т. д.) Не все представляют, что при этом происходит под капотом, – как именно определяется новая форма DOM-элемента.Каждый трансформируемый фрагмент (HTML-элемент или часть изображения на canvas) – это всего лишь набор отдельных точек (пикселей). Можно выделить несколько базовых характеристик такого фрагмента:
e,f– координаты, положение фрагмента относительно целого холста (веб-страницы или элемента canvas).a,d– размеры (ширина и высота) одного пикселя.
Изначально e и f равны 0 (фрагмент никуда не сдвинут с исходной точки), а размеры пикселя (a, d) равны 1 (то есть 100% от исходного).
При отрисовке каждый пиксель отображается последовательно в нужной позиции и с нужным размером.
Если мы установим e = 20, то каждый пиксель фрагмента будет отрисован на 20 пикселей по горизонтали правее – изображение сместится.

Если же установить a = 2, то каждый пиксель по горизонтали будет вдвое больше, чем по вертикали, и изображение растянется в ширину.
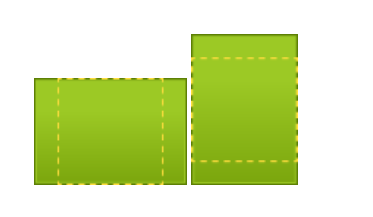
Сдвиг пикселей относительно друг друга
Кроме простых трансформаций масштабирования и сдвига всего фрагмента, есть еще пиксельный сдвиг. Он задается с помощью коэффициента, на который умножаются исходные координаты каждого пикселя для расчета его новой позиции.
b– коэффициент сдвига по вертикалиc– коэффициент сдвига по горизонтали
По умолчанию пиксельный сдвиг равен нулю, но если изменить его, то можно получить эффект наклона фрагмента.

- Сдвиг по горизонтали (
c) умножается наy-координату пикселя, то есть каждый следующий ряд пикселей сдвигается по горизонтали относительно предыдущего. - Сдвиг по вертикали (
b) соответственно умножается наx-координату пикселя, то есть каждая следующая колонка пикселей сдвигается по вертикали относительно предыдущей.
Предположим, что величина сдвига по горизонтали c = 5. Весь первый ряд пикселей останется на своем месте, так как их координата y равна нулю. Зато второй ряд (с координатой y=1) сползает вправо на 5 (1 * 5) пикселей. Третий ряд сдвинется уже на 10 пикселей, относительно исходной позиции.
Матрицы трансформаций
Все параметры трансформации фрагмента обычно представлены в виде матрицы. Для двумерного пространства она выглядит вот так:
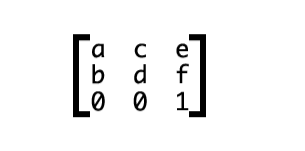
- a – горизонтальный размер пикселя (масштаб)
- b – горизонтальный сдвиг пикселей (деформация по оси OX)
- c – вертикальный сдвиг пикселей (деформация по оси OY)
- d – вертикальный размер пикселя (масштаб)
- e – горизонтальное смещение фрагмента (сдвиг)
- f – вертикальное смещение фрагмента (сдвиг)
Координаты же каждого пикселя в 2d-пространстве можно представить как вектор:
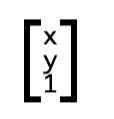
Чтобы вычислить координаты пикселя после трансформации, нужно умножить матрицу трансформации на его текущие координаты:
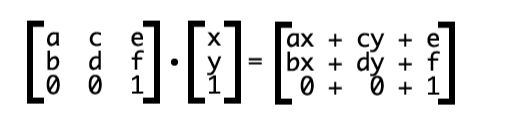
В результате получается вектор с новыми координатами пикселя.
Реализация
Умножение матриц осуществляется по правилу "строка на столбец", реализуем это на JavaScript:
function apply2dTransform(matrix, vector) {
return matrix.map(row => {
return row.reduce((sum, param, i) => {
return sum + (param * vector[i])
}, 0)
});
}
Возьмем из фрагмента пиксель с координатами x = 10, y = 10 и опробуем на нем разные матрицы трансформации:
let pixel = [ 10, 10, 1 ];
Дефолтная матрица (без трансформаций)
let defaultMatrix = [
[ 1, 0, 0 ],
[ 0, 1, 0 ],
[ 0, 0, 1]
]
// координаты пикселя не изменились
apply2dTransform(defaultMatrix, pixel); // [ 10, 10, 1]
Матрица сдвига
let shiftMatrix = [
[ 1, 0, 20 ],
[ 0, 1, 50 ],
[ 0, 0, 1]
]
apply2dTransform(shiftMatrix, pixel); // [ 30, 60, 1]
Трансформация поворота
Можно изменять разные параметры одновременно, чтобы получать более сложные трансформации. Например, трансформация поворота – это сочетание сдвига пикселей и масштабирования. Для поворота на угол A (против часовой стрелки) требуется такая матрица:
let rotateMatrix = [
[ Math.cos(A), Math.sin(A), 0 ],
[ -Math.sin(A), Math.cos(A), 0 ],
[ 0, 0, 1]
]
Попробуем применить ее к нашему пикселю:
function createRotateMatrix(deg) {
let rad = deg * Math.PI / 180; // угол в радианах
return [
[ Math.cos(rad), Math.sin(rad), 0 ],
[ -Math.sin(rad), Math.cos(rad), 0 ],
[ 0, 0, 1]
]
}
apply2dTransform(createRotateMatrix(90), pixel); // [ 10, -10, 1 ]
В трехмерном пространстве трансформации сложнее, так как прибавляется еще одно измерение и увеличивается размерность матриц, однако суть у них та же самая.
Заключение
Теперь вы имеет представление о всех основных способах работы с данными в JavaScript. Выбирая структуры и алгоритмы для очередной задачи, помните:
Умные структуры данных и тупой код работают куда лучше, чем наоборот.
Другие статьи цикла:
- Часть 1. Основные понятия и работа с массивами
- Часть 2. Стеки, очереди и связные списки
- Часть 3. Деревья
- Часть 4. Графы
- Часть 5. Объекты и хеширование




О каких еще алгоритмах стоит рассказать подробнее?