Если хочешь подтянуть свои знания, загляни на наш курс «Алгоритмы и структуры данных», на котором ты:
- углубишься в решение практических задач;
- узнаешь все про сложные алгоритмы, сортировки, сжатие данных и многое другое.
Ты также будешь на связи с преподавателем и другими студентами.
В итоге будешь браться за сложные проекты и повысишь чек за свою работу 🙂
Другие статьи цикла:
- Часть 1. Основные понятия и работа с массивами
- Часть 2. Стеки, очереди и связные списки
- Часть 4. Графы
- Часть 5. Объекты и хеширование
- Часть 6. Полезные алгоритмы для веб-разработки
Структура данных «Дерево»
В самом начале изучения деревья могут сбивать с толку, ведь они используют совсем другой способ упорядочивания данных – иерархический. Но хотя это и может показаться сложным, на практике это обычно оборачивается профитом, так как деревья позволяют применять более эффективные алгоритмы.
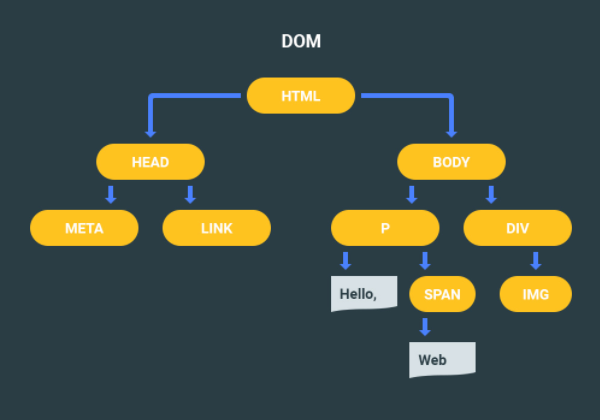
Структура дерево очень активно используется в разработке, например, всеми любимый DOM – это дерево. В виде дерева можно представить, например, иерархию должностей в компании или каталог библиотеки.
Устройство дерева
В отличие от обычных деревьев, структура данных дерево растет сверху вниз – ее корень находится на самом верху – так удобнее изображать.
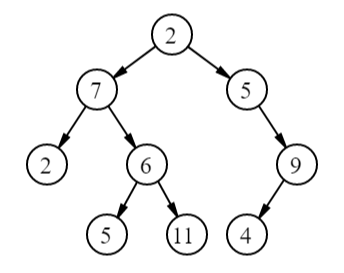
- У корневого элемента (на картинке узел со значением 2) есть несколько дочерних узлов (7 и 5), каждый из которых в свою очередь сам является корнем поддерева. Таких уровней может быть сколько угодно.
- Элемент, у которого нет дочерних узлов, называется листом, или терминальным узлом (2, 5, 11, 4). Все остальные узлы (кроме корневого), у которых есть потомки, называются внутренними.
- Каждый узел дерева имеет только одного родителя, не больше. Кроме корневого узла, у которого родителей нет вообще.
- Высота дерева – длина самой длинной ветви (количество ребер). У дерева на картинке она равна 3 – ветка от корня 2 до листа 5. Высоту также можно найти для любого внутреннего узла, например, для узла 6 высота равна 1.
Кроме двоичных, широкое практическое применение имеют деревья с четырьмя узлами (дерево квадрантов). Они используются в геймдеве для организации сетки. Каждый узел в таком дереве представляет одно направление (север-запад, юго-восток и так далее).
Основные операции
Деревья – довольно сложные структуры. Для работы с иерархическими данными они должны предоставлять ряд алгоритмов.
Основные операции, которые нам нужны:
- Добавление нового узла (
add); - Удаление узла по его значению (
remove); - Поиск узла по значению (
find); - Обход всех элементов (
traverse).
При необходимости этот список можно расширить более сложными алгоритмами:
- Вставка/удаление поддерева;
- Вставка/удаление ветви;
- Вставка элемента в определенную позицию;
- Поиск наименьшего общего предка для двух узлов.
В этой статье мы рассмотрим только основные алгоритмы работы с деревьями, а более продвинутые вы сможете реализовать сами на их основе.
Реализация дерева на JavaScript
Мы реализуем дерево, начиная с корневого узла. Каждый узел будет содержать собственное значение, а также ссылки на дочерние элементы (на левый и на правый) и на родителя. Это очень похоже на связный список, который мы разбирали в прошлой статье.
class BinaryTreeNode {
constructor(value) {
this.left = null;
this.right = null;
this.parent = parent;
this.value = value;
}
get height() {
let leftHeight = this.left ? this.left.height + 1 : 0;
let rightHeight = this.right ? this.right.height + 1 : 0;
return Math.max(leftHeight, rightHeight);
}
}
let tree = new BinaryTreeNode('a');
Высота узла (height) вычисляется рекурсивно, на основе высоты его дочерних узлов.
Добавление узлов
Первый алгоритм, который мы должны реализовать для дерева, – это вставка новых узлов. Самая простая реализация не предъявляет никаких правил к расположению элементов, поэтому мы можем просто приписать новый узел к существующему как дочерний (с нужной стороны).
class BinaryTreeNode {
// …
setLeft(node) {
if (this.left) {
this.left.parent = null;
}
if (node) {
this.left = node;
this.left.parent = this;
}
}
setRight(node) {
if (this.right) {
this.right.parent = null;
}
if (node) {
this.right = node;
this.right.parent = this;
}
}
}
При вставке важно обновить все затронутые ссылки: left или right для родительского узла и parent для дочернего. Если у родителя уже был потомок, его свойство parent нужно обнулить.
Создание дерева
Реализация очень простая, но с ее помощью мы уже можем построить настоящее двоичное дерево, например, такое как на картинке:
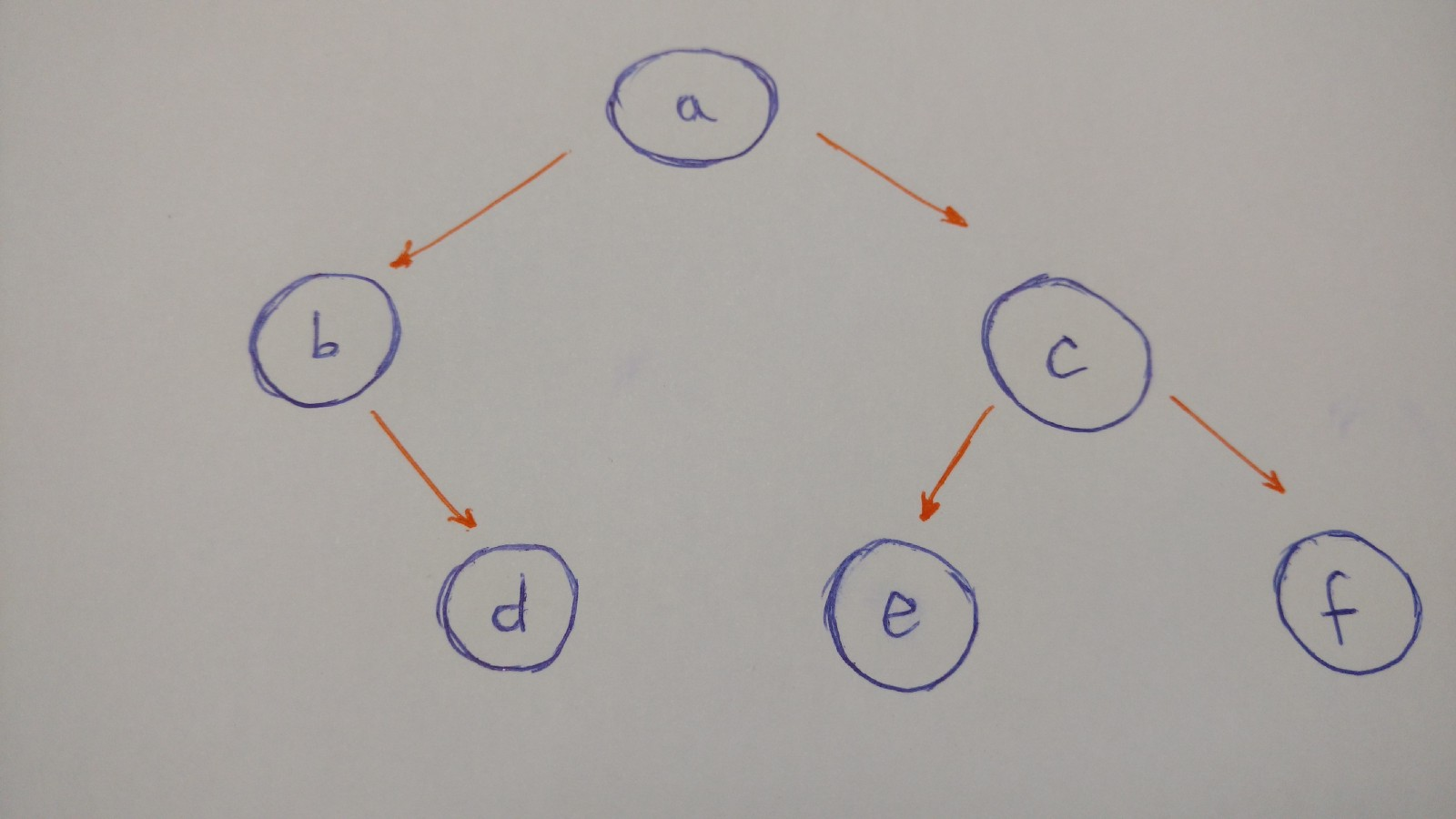
let aNode = new BinaryTreeNode('a');
let bNode = new BinaryTreeNode('b');
aNode.setLeft(bNode);
let cNode = new BinaryTreeNode('c');
aNode.setRight(cNode);
let dNode = new BinaryTreeNode('d');
bNode.setRight(dNode);
let eNode = new BinaryTreeNode('e');
cNode.setLeft(eNode);
let fNode = new BinaryTreeNode('f');
cNode.setRight(fNode);
Обход дерева
Теперь нам нужен способ обойти все узлы дерева, чтобы выполнить для каждого из них какую-либо операцию.
Мы разберем два популярных алгоритма обхода дерева:
- поиск в глубину (depth-first search);
- поиск в ширину (breadth-first search).
DFS: Поиск в глубину
Алгоритм начинает с корневого узла и последовательно проверяет все исходящие из него ребра. Если ребро ведет в вершину, которая ранее не рассматривалась, то алгоритм рекурсивно запускается уже для нее, а после его выполнения продолжается проверка других ребер. Таким образом последовательно осматривается каждая ветка дерева.
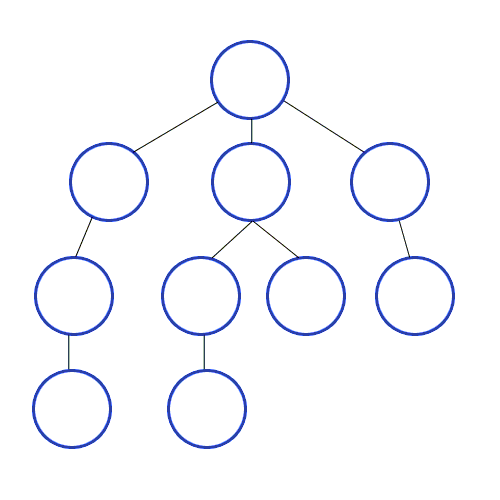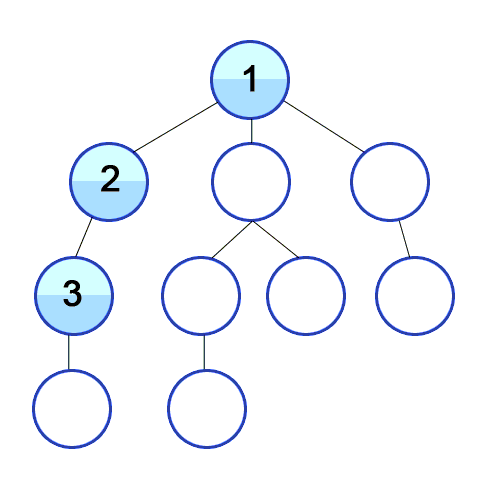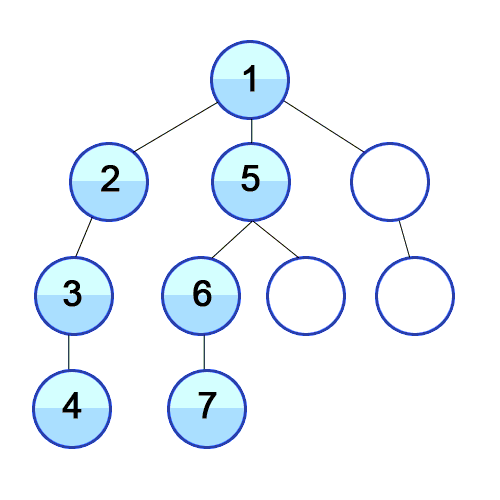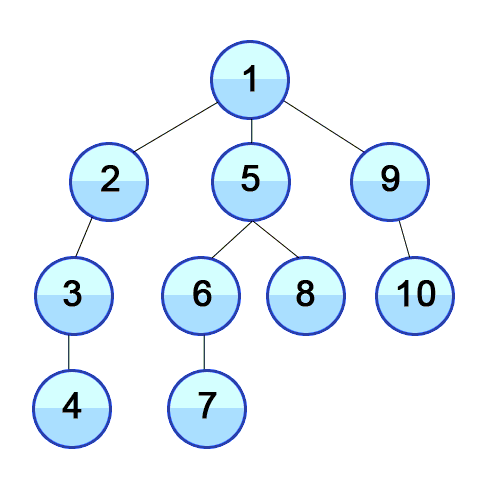
function traverseDFRecursive(node, callback) {
// выполнение коллбэка для самого узла
callback(node);
// выполнение коллбэка для левого потомка
if (node.left) {
traverseDFRecursive(node.left, callback);
}
// выполнение коллбэка для правого потомка
if (node.right) {
traverseDFRecursive(node.right, callback);
}
}
function traverseDF(root, callback) {
traverseDFRecursive(root, callback);
}
Запустим перебор для нашего бинарного дерева:
traverseDF(aNode, node => console.log(node.value));
В консоли мы увидим следующее:

Существует три модификации алгоритма с разным способом перебора узлов:
- обход в прямом порядке, или предупорядоченный обход (pre-order walk). Перебор начинается с родительского узла и идет вниз, к дочерним.
- обход в обратном порядке, или поступорядоченный (post-order walk). Сначала перебираем левого и правого потомков, а потом родителя.
- симметричный обход. Начинаем с левого потомка, потом родитель, потом правый потомок.
Мы реализовали обход в прямом порядке, но можно использовать и другие способы.
BFS: Поиск в ширину
Алгоритм начинает с корневого узла (первый уровень) и двигается по всем ребрам, выходящим из него, перебирая последовательно каждый дочерний элемент (второй уровень). Когда все ребра проверены, алгоритм переходит на следующий уровень и начинает перебирать дочерние элементы дочерних элементов (элементы третьего уровня) и так далее.
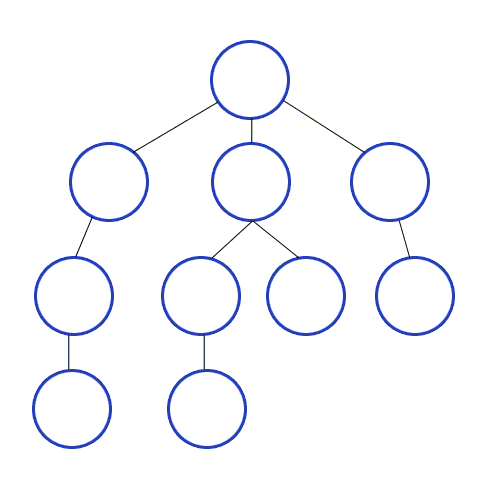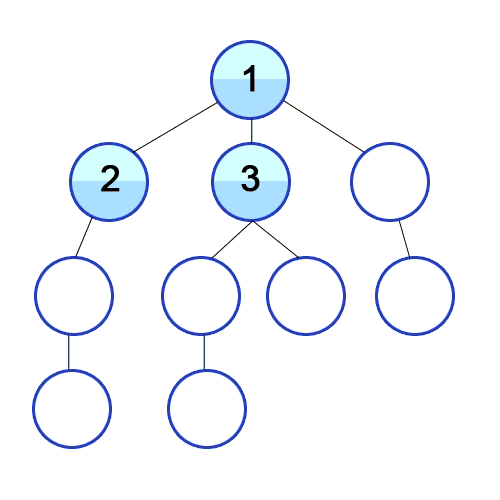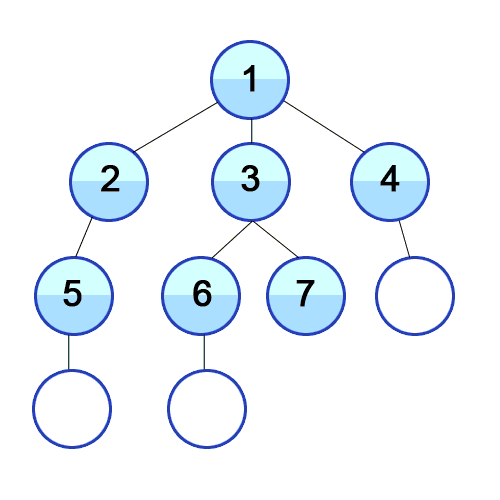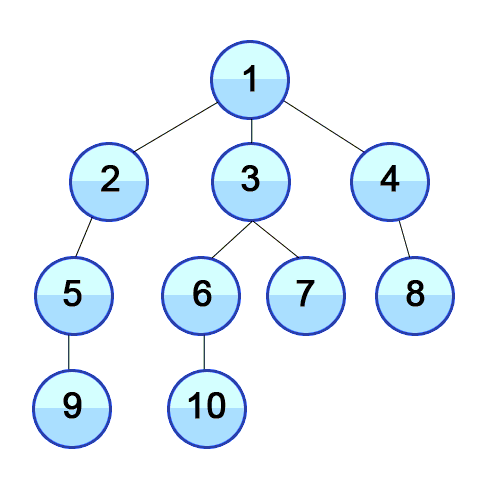
Для реализации алгоритма обхода дерева в ширину мы будем использовать структуру данных очередь, которую уже разбирали в предыдущей статье цикла. На каждом шаге извлекаем из нее элемент, который был добавлен первым и перебираем всех его потомков. Каждый потомок также добавляется в очередь.
Можно использовать реализацию очереди из предыдущей статьи или воспользоваться простой очередью на базе JavaScript-массива.
class Queue {
constructor() {
this.arr = [];
}
enqueue(value) {
this.arr.push(value);
}
dequeue() {
return this.arr.shift();
}
isEmpty() {
return this.arr.length == 0;
}
}
function traverseBF(root, callback) {
let nodeQueue = new Queue();
nodeQueue.enqueue(root);
while(!nodeQueue.isEmpty()) {
let currentNode = nodeQueue.dequeue();
// Вызываем коллбэк для самого узла
callback(currentNode);
// Добавляем в очередь левого потомка
if (currentNode.left) {
nodeQueue.enqueue(currentNode.left);
}
// Добавляем в очередь правого потомка
if (currentNode.right) {
nodeQueue.enqueue(currentNode.right);
}
}
}
Запустим перебор в ширину:
traverseBF(aNode, node => console.log(node.value));
Результат выглядит так:

Бинарное дерево поиска
Двоичное (бинарное) дерево поиска (binary search tree, BST) – это дерево, в котором элементы размещаются согласно определенному правилу (упорядоченно):
- Каждый узел должен быть "больше" любого элемента в своем левом поддереве.
- Каждый узел должен быть "меньше" любого элемента в своем правом поддереве.
Слова "больше" и "меньше" соответственно означают результат сравнения двух узлов функцией-компаратором.
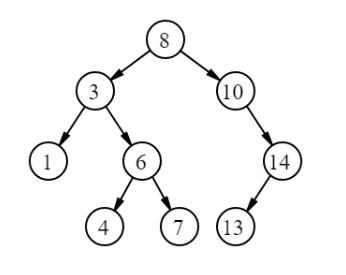
Благодаря такой сортировке мы можем использовать все преимущества стратегии "разделяй и властвуй" – при поиске элемента можно смело отбрасывать половину дерева. Такие алгоритмы работают гораздо быстрее, чем линейный перебор каждого узла.
Реализация на JavaScript
Для создания бинарного дерева поиска мы используем уже готовый класс BinaryTreeNode, немного его расширив. Необходимо добавить метод insert, определяющий логику вставки нового узла для сохранения сортировки. Также создадим отдельный класс для самого дерева, который будет хранить ссылку на корневой элемент и делегировать ему рекурсивное выполнение различных методов.
Так как бинарное дерево поиска является упорядоченным, нам еще потребуется функция-компаратор для сравнения элементов.
class BinarySearchTreeNode extends BinaryTreeNode {
constructor(value, comparator) {
super(value);
this.comparator = comparator;
}
insert(value) {
if (this.comparator(value, this.value) < 0) {
if (this.left) return this.left.insert(value);
let newNode = new BinarySearchTreeNode(value, this.comparator);
this.setLeft(newNode);
return newNode;
}
if (this.comparator(value, this.value) > 0) {
if (this.right) return this.right.insert(value);
let newNode = new BinarySearchTreeNode(value, this.comparator);
this.setRight(newNode);
return newNode;
}
return this;
}
}
class BinarySearchTree {
constructor(value, comparator) {
this.root = new BinarySearchTreeNode(value, comparator);
this.comparator = comparator;
}
insert(value) {
this.root.insert(value);
}
}
Метод insert, сравнивает значение нового элемента со значением узла и определяет, в какое поддерево его нужно поместить.
Создадим дерево как на картинке выше:
const tree = new BinarySearchTree(8, (a, b) => a - b);
tree.insert(3);
tree.insert(10);
tree.insert(14);
tree.insert(1);
tree.insert(6);
tree.insert(4);
tree.insert(7);
tree.insert(13);
А теперь обойдем все его элементы, чтобы убедиться, что оно сформировано правильно:
traverseBF(tree.root);
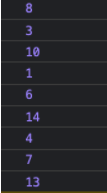
Поиск в бинарном дереве поиска
Алгоритм поиска в BST очень похож на двоичный поиск в отсортированном массиве, который мы разбирали в первой части цикла. Сравниваем искомое значение с корневым узлом, определяем, в каком поддереве нужно искать, а второе поддерево просто отбрасываем.
class BinarySearchTree {
find(value) {
return this.root.find(value);
}
}
class BinarySearchTreeNode {
find(value) {
if (this.comparator(this.value, value) === 0) return this;
if (this.comparator(this.value, value) < 0 && this.left) {
return this.left.find(value);
}
if (this.comparator(this.value, value) > 0 && this.right) {
return this.right.find(value);
}
return null;
}
}
Алгоритм поиска рекурсивно проверяет все узлы, пока не найдет подходящий.
Удаление узлов
Удаление узлов из BST – это достаточно сложный алгоритм, так как после удаления узла необходимо восстановить структуру дерева, чтобы оно оставалось отсортированным.
Есть три сценария:
- У удаляемого узла нет потомков (листовой узел).
- У удаляемого узла один потомок (левый или правый).
- У удаляемого узла два потомка.
- Первый случай самый простой и не требует перестройки дерева после удаления.
- Во втором случае после удаления нужно установить связь между родителем удаленного узла и его потомком. Все потомки удаленного узла в любом случае находятся с той же стороны от его родителя, что и сам узел. Поэтому мы записываем их с той же стороны, на которой находился удаленный узел.
- Третий случай самый сложный. Мы должны найти следующий по порядку узел (минимальный узел в правом поддереве удаляемого узла) и поставить его вместо удаляемого.
Для реализации алгоритма удаления нам понадобится несколько вспомогательных методов.
class BinarySearchTreeNode {
// ...
findMin() {
if (!this.left) {
return this;
}
return this.left.findMin();
}
removeChild(nodeToRemove) {
if (this.left && this.left === nodeToRemove) {
this.left = null;
return true;
}
if (this.right && this.right === nodeToRemove) {
this.right = null;
return true;
}
return false;
}
replaceChild(nodeToReplace, replacementNode) {
if (!nodeToReplace || !replacementNode) {
return false;
}
if (this.left && this.left === nodeToReplace) {
this.left = replacementNode;
return true;
}
if (this.right && this.right === nodeToReplace) {
this.right = replacementNode;
return true;
}
return false;
}
}
findMinищет минимальный элемент в поддереве.removeChildудаляет указанный элемент, если он является дочерним для данного узла.replaceChildзаменяет дочерний элемент на новый.
Теперь добавим в класс BinarySearchTree новый метод remove:
class BinarySearchTree {
//...
insert(value) {
if (!this.root.value) this.root.value = value;
else this.root.insert(value);
}
remove(value) {
const nodeToRemove = this.find(value);
if (!nodeToRemove) {
throw new Error('Item not found');
}
const parent = nodeToRemove.parent;
// Нет потомков, листовой узел
if (!nodeToRemove.left && !nodeToRemove.right) {
if (parent) {
// Удалить у родителя указатель на удаленного потомка
parent.removeChild(nodeToRemove);
} else {
// Нет родителя, корневой узел
nodeToRemove.value = undefined;
}
}
// Есть и левый, и правый потомки
else if (nodeToRemove.left && nodeToRemove.right) {
// Ищем минимальное значение в правом поддереве
// И ставим его на место удаляемого узла
const nextBiggerNode = nodeToRemove.right.findMin();
if (this.comparator(nextBiggerNode, nodeToRemove.right) === 0) {
// Правый потомок одновременно является минимальным в правом дереве
// то есть у него нет левого поддерева
// можно просто заменить удаляемый узел на его правого потомка
nodeToRemove.value = nodeToRemove.right.value;
nodeToRemove.setRight(nodeToRemove.right.right);
} else {
// Удалить найденный узел (рекурсия)
this.remove(nextBiggerNode.value);
// Обновить значение удаляемого узла
nodeToRemove.value = nextBiggerNode.value;
}
}
// Есть только один потомок (левый или правый)
else {
// Заменить удаляемый узел на его потомка
const childNode = nodeToRemove.left || nodeToRemove.right;
if (parent) {
parent.replaceChild(nodeToRemove, childNode);
} else {
this.root = childNode;
}
}
// Удалить ссылку на родителя
nodeToRemove.parent = null;
return true;
}
}
Обратите внимание, в результате удаления возможна ситуация, в которой дерево остается пустым (удаляется корневой элемент, не имеющий потомков). В этом случае мы просто удаляем значение элемента root. Из-за этого требуется небольшая доработка метода insert: если у корневого элемента нет значения, мы просто присваиваем ему новое.
Полный код
Полная реализация бинарного дерева поиска на JavaScript:
class BinarySearchTreeNode extends BinaryTreeNode {
constructor(value, comparator) {
super(value);
this.comparator = comparator;
}
insert(value) {
if (this.comparator(value, this.value) < 0) {
if (this.left) return this.left.insert(value);
let newNode = new BinarySearchTreeNode(value, this.comparator);
this.setLeft(newNode);
return newNode;
}
if (this.comparator(value, this.value) > 0) {
if (this.right) return this.right.insert(value);
let newNode = new BinarySearchTreeNode(value, this.comparator);
this.setRight(newNode);
return newNode;
}
return this;
}
find(value) {
if (this.comparator(this.value, value) === 0) return this;
if (this.comparator(this.value, value) < 0 && this.left) {
return this.left.find(value);
}
if (this.comparator(this.value, value) > 0 && this.right) {
return this.right.find(value);
}
return null;
}
findMin() {
if (!this.left) {
return this;
}
return this.left.findMin();
}
removeChild(nodeToRemove) {
if (this.left && this.left === nodeToRemove) {
this.left = null;
return true;
}
if (this.right && this.right === nodeToRemove) {
this.right = null;
return true;
}
return false;
}
replaceChild(nodeToReplace, replacementNode) {
if (!nodeToReplace || !replacementNode) {
return false;
}
if (this.left && this.left === nodeToReplace) {
this.left = replacementNode;
return true;
}
if (this.right && this.right === nodeToReplace) {
this.right = replacementNode;
return true;
}
return false;
}
}
class BinarySearchTree {
constructor(value, comparator) {
this.root = new BinarySearchTreeNode(value, comparator);
this.comparator = comparator;
}
insert(value) {
if (!this.root.value) this.root.value = value;
else this.root.insert(value);
}
find(value) {
return this.root.find(value);
}
remove(value) {
const nodeToRemove = this.find(value);
if (!nodeToRemove) {
throw new Error('Item not found');
}
const parent = nodeToRemove.parent;
// Нет потомков, листовой узел
if (!nodeToRemove.left && !nodeToRemove.right) {
if (parent) {
// Удалить у родителя указатель на удаленного потомка
parent.removeChild(nodeToRemove);
} else {
// Нет родителя, корневой узел
nodeToRemove.value = undefined;
}
}
// Есть и левый, и правый потомки
else if (nodeToRemove.left && nodeToRemove.right) {
// Ищем минимальное значение в правом поддереве
// И ставим его на место удаляемого узла
const nextBiggerNode = nodeToRemove.right.findMin();
if (this.comparator(nextBiggerNode, nodeToRemove.right) === 0) {
// Правый потомок одновременно является минимальным в правом дереве
// то есть у него нет левого поддерева
// можно просто заменить удаляемый узел на его правого потомка
nodeToRemove.value = nodeToRemove.right.value;
nodeToRemove.setRight(nodeToRemove.right.right);
} else {
// Удалить найденный узел (рекурсия)
this.remove(nextBiggerNode.value);
// Обновить значение удаляемого узла
nodeToRemove.value = nextBiggerNode.value;
}
}
// Есть только один потомок (левый или правый)
else {
// Заменить удаляемый узел на его потомка
const childNode = nodeToRemove.left || nodeToRemove.right;
if (parent) {
parent.replaceChild(nodeToRemove, childNode);
} else {
this.root = childNode;
}
}
// Удалить ссылку на родителя
nodeToRemove.parent = null;
return true;
}
}
Эффективность
Временная сложность всех основных операций в бинарном дереве составляет log(n) – это довольно эффективная структура данных.
| Индексация | Поиск | Вставка | Удаление |
| O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) |
Сбалансированные бинарные деревья
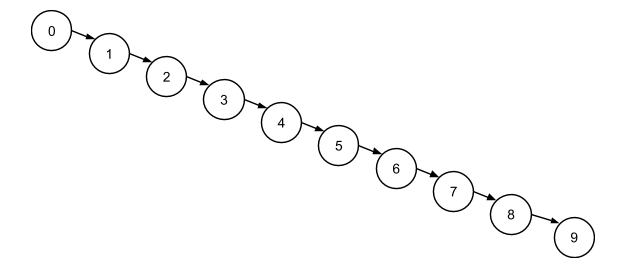
На картинке изображено валидное бинарное дерево поиска. Для каждого узла соблюдается правило: все узлы в правом поддереве имеют большее значение. Однако такое дерево не позволяет нам пользоваться преимуществами стратегии "разделяй и властвуй", ведь тут нечего отбрасывать. Говорят, что дерево выродилось в список.
Чтобы избежать таких ситуаций, используются более сложные структуры данных – самобалансирующиеся деревья:
Эти деревья используют различные алгоритмы "выравнивания" при вставке и удалении элементов.
Легким движением руки несбалансированное дерево поиска превращается в сбалансированное:

Визуализация самобалансирующихся деревьев:
Двоичная куча
У кучи также есть корень, а элементы могут иметь дочерние узлы. У двоичной кучи каждый узел может иметь не более двух потомков.
Как и бинарное дерево поиска, куча имеет определенные требования к размещению элементов: все потомки узла должны быть меньше его. Куча, соответствующая этому правилу, называется max-кучей. В ней корень всегда является максимальным элементом.
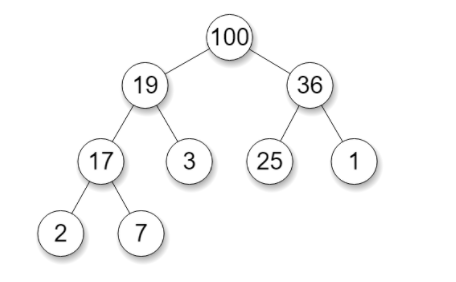
Бывают также min-кучи, которые следуют противоположному правилу: все потомки узла должны быть больше его. Таким образом, корнем всегда оказывается минимальный элемент кучи.
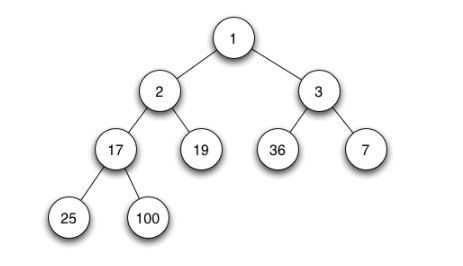
По сути, куча – это очередь с приоритетом. Каждый новый элемент размещается в этой очереди в соответствии с его приоритетом, чем приоритет выше, тем ближе он к началу очереди.
Каждую кучу можно представить в виде линейного массива:
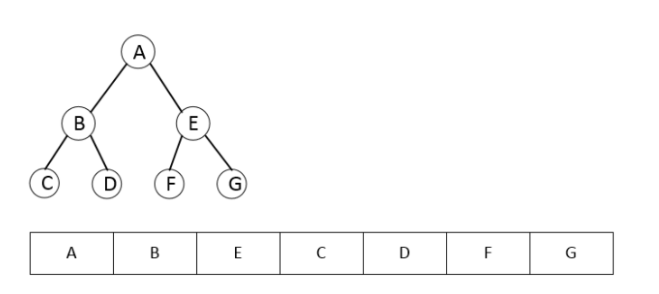
Чаще всего используется именно линейная реализация, однако дерево более наглядно демонстрирует принцип распределения.
Основные операции
Базовые операции с кучей такие же, как и с очередью:
- найти элемент с максимальным приоритетом (максимальный элемент в max-куче или минимальный элемент в min-куче);
- удалить элемент с максимальным приоритетом;
- добавить в очередь новый элемент.
Реализация
Мы реализуем на JavaScript min-кучу. Для max-кучи нужно только изменить операцию сравнения.
class Heap {
constructor(comparator) {
this.arr = [];
this.comparator = comparator;
}
isCorrectOrder(first, second) {
return this.comparator(first, second) < 0;
}
}
Так как элементы кучи хранятся в виде массива по уровням, нужно определить вспомогательные методы для нахождения потомков и родителей конкретного узла. Мы можем это сделать, так как куча является полным деревом, то есть не имеет пропусков в своей структуре. Индекс нужного элемента в массиве можно вычислить, исходя из его позиции в дереве.
class Heap {
// ...
getLeftChildIndex(parentIndex) {
return (2 * parentIndex) + 1;
}
getRightChildIndex(parentIndex) {
return (2 * parentIndex) + 2;
}
getParentIndex(childIndex) {
return Math.floor((childIndex - 1) / 2);
}
leftChild(parentIndex) {
return this.arr[this.getLeftChildIndex(parentIndex)];
}
rightChild(parentIndex) {
return this.arr[this.getRightChildIndex(parentIndex)];
}
parent(childIndex) {
return this.arr[this.getParentIndex(childIndex)];
}
}
Добавим еще несколько вспомогательных методов для удобных проверок:
class Heap {
// ...
hasParent(childIndex) {
return this.getParentIndex(childIndex) >= 0;
}
hasLeftChild(parentIndex) {
return this.getLeftChildIndex(parentIndex) < this.arr.length;
}
hasRightChild(parentIndex) {
return this.getRightChildIndex(parentIndex) < this.arr.length;
}
isEmpty() {
return !this.arr.length;
}
}
Добавление элемента
Сначала новый элемент помещается в самый конец кучи (конец массива), как и в обычной очереди, а затем начинается процесс его поднятия вверх с учетом приоритета. Это рекурсивный алгоритм, который сравнивает элемент с предыдущим и при необходимости меняет их местами.
class Heap {
// ...
push(item) {
this.arr.push(item);
this.heapifyUp();
return this;
}
heapifyUp(startIndex) {
let currentIndex = startIndex || this.arr.length - 1;
while (
this.hasParent(currentIndex)
&& !this.isCorrectOrder(this.parent(currentIndex), this.arr[currentIndex])
) {
let parentIndex = this.getParentIndex(currentIndex);
this.swap(currentIndex, parentIndex);
currentIndex = parentIndex;
}
}
swap(indexOne, indexTwo) {
const tmp = this.arr[indexTwo];
this.arr[indexTwo] = this.arr[indexOne];
this.arr[indexOne] = tmp;
}
}
Получение элемента с максимальным приоритетом
Для получения элемента с начала очереди может быть два метода:
peek– просмотр без удаления;pop– получение элемента и удаление его из очереди.
С peek все понятно, нам просто нужно взять нулевой элемент массива. А вот после удаления необходимо перебалансировать дерево. Для этого мы берем самый последний элемент массива, ставим его в начало и начинаем сдвигать вниз, последовательно сравнивая с его дочерними элементами.
class Heap {
// ...
peek() {
if (this.arr.length === 0) {
return null;
}
return this.arr[0];
}
pop() {
if (this.arr.length === 0) {
return null;
}
if (this.arr.length === 1) {
return this.arr.pop();
}
const item = this.arr[0];
this.arr[0] = this.arr.pop();
this.heapifyDown();
return item;
}
heapifyDown(customStartIndex = 0) {
let currentIndex = customStartIndex;
let nextIndex = null;
while (this.hasLeftChild(currentIndex)) {
if (
this.hasRightChild(currentIndex)
&& this.isCorrectOrder(this.rightChild(currentIndex), this.leftChild(currentIndex))
) {
nextIndex = this.getRightChildIndex(currentIndex);
} else {
nextIndex = this.getLeftChildIndex(currentIndex);
}
if (this.isCorrectOrder(
this.arr[currentIndex],
this.arr[nextIndex],
)) {
break;
}
this.swap(currentIndex, nextIndex);
currentIndex = nextIndex;
}
}
}
Полный код
class Heap {
constructor(comparator) {
this.arr = [];
this.comparator = comparator;
}
isCorrectOrder(first, second) {
return this.comparator(first, second) < 0;
}
getLeftChildIndex(parentIndex) {
return (2 * parentIndex) + 1;
}
getRightChildIndex(parentIndex) {
return (2 * parentIndex) + 2;
}
getParentIndex(childIndex) {
return Math.floor((childIndex - 1) / 2);
}
leftChild(parentIndex) {
return this.arr[this.getLeftChildIndex(parentIndex)];
}
rightChild(parentIndex) {
return this.arr[this.getRightChildIndex(parentIndex)];
}
parent(childIndex) {
return this.arr[this.getParentIndex(childIndex)];
}
hasParent(childIndex) {
return this.getParentIndex(childIndex) >= 0;
}
hasLeftChild(parentIndex) {
return this.getLeftChildIndex(parentIndex) < this.arr.length;
}
hasRightChild(parentIndex) {
return this.getRightChildIndex(parentIndex) < this.arr.length;
}
isEmpty() {
return !this.arr.length;
}
swap(indexOne, indexTwo) {
const tmp = this.arr[indexTwo];
this.arr[indexTwo] = this.arr[indexOne];
this.arr[indexOne] = tmp;
}
push(item) {
this.arr.push(item);
this.heapifyUp();
return this;
}
heapifyUp(startIndex) {
let currentIndex = startIndex || this.arr.length - 1;
while (
this.hasParent(currentIndex)
&& !this.isCorrectOrder(this.parent(currentIndex), this.arr[currentIndex])
) {
let parentIndex = this.getParentIndex(currentIndex);
this.swap(currentIndex, parentIndex);
currentIndex = parentIndex;
}
}
peek() {
if (this.arr.length === 0) {
return null;
}
return this.arr[0];
}
pop() {
if (this.arr.length === 0) {
return null;
}
if (this.arr.length === 1) {
return this.arr.pop();
}
const item = this.arr[0];
this.arr[0] = this.arr.pop();
this.heapifyDown();
return item;
}
heapifyDown(customStartIndex = 0) {
let currentIndex = customStartIndex;
let nextIndex = null;
while (this.hasLeftChild(currentIndex)) {
if (
this.hasRightChild(currentIndex)
&& this.isCorrectOrder(this.rightChild(currentIndex), this.leftChild(currentIndex))
) {
nextIndex = this.getRightChildIndex(currentIndex);
} else {
nextIndex = this.getLeftChildIndex(currentIndex);
}
if (this.isCorrectOrder(
this.arr[currentIndex],
this.arr[nextIndex],
)) {
break;
}
this.swap(currentIndex, nextIndex);
currentIndex = nextIndex;
}
}
}
Заключение
Деревья – довольно сложная (по сравнению с линейными), но очень интересная структура данных. Об одном из самых популярных ее применений (поиске данных) мы уже поговорили.
В следующей статье мы пойдем еще дальше и поговорим самой нелинейной структуре – графах – и алгоритмах работы с ней.
Больше полезной информации вы найдете на наших телеграм-каналах «Библиотека программиста» и «Книги для программистов».



Комментарии