Эта публикация представляет собой перевод статьи Тайлера Хоббса – художника, использующего в своих работах алгоритмы и программирование. Учитывая специфику Библиотеки программиста, перевод незначительно сокращён. Описанные в статье идеи можно использовать для реализации собственных проектов выходного дня, связанных с созданием эксклюзивных графических узоров для веба и офлайновых продуктов.

Векторное поле – мощный и гибкий инструмент для создания интересных изображений. Это то, к чему многие программисты приходят, когда делают первые алгоритмические рисунки. Но мало кто находит время, чтобы исследовать всё разнообразие способов применения векторных полей. В статье изложены базовые сведения о векторных полях, варианты их применения и советы, как получить сбалансированное изображение.

Сетка углов

Векторное поле строится на сетке, целиком покрывающей изображение, в каждой точке сетки задаётся значение угла. В памяти компьютера сетка представлена двумерным массивом чисел с плавающей запятой.

Шаг. При инициализации сетки вы выбираете шаг – расстояние между соседними элементами. Чем выше разрешение, тем меньше шаг, мельче создаваемые детали и линии получаются более плавными. Но с уменьшением шага падает производительность. В качестве отправной точки шага подойдёт порядок 0.5% ширины изображения. Для шага лучше использовать целочисленные значения, чтобы избежать ошибок округления чисел с плавающей запятой.

Границы. Последнее, что надо настроить – границы сетки. Возникает соблазн сравнять их с границами изображения. Но лучше границы сетки отдалить от границ кадра. Иначе край изображения будет сильно влиять на «течение» векторного поля. За счёт отдаления границ сетки мы как бы фотографируем поток, не воздействуя на его течение. Иногда даже лучше начать кривые вне изображения и позволить им течь в него.

Пишем псевдокод. Давайте предположим, что у нас есть изображение размером 1000 x 1000 пикселей, и мы хотим добавить 50%-ный запас пространства за пределами изображения. Мы можем инициализировать нашу сетку примерно таким образом:

        left_x = int(width * -0.5)
right_x = int(width * 1.5)
top_y = int(height * -0.5)
bottom_y = int(height * 1.5)

resolution = int(width * 0.01) 

num_columns = (right_x - left_x) / resolution
num_rows = (bottom_y - top_y) / resolution

grid = float[num_columns][num_rows]

default_angle = PI * 0.25

for (column in num_columns) {
    for (row in num_rows) {
        grid[column][row] = default_angle
    }
}
    

При запуске программы визуализации в этом состоянии, сетка будет выглядеть примерно так:

Теперь у нас есть поле, с которым можно работать. К сожалению, на нём пока можно рисовать только прямые линии. Давайте немного изогнём его, изменив описание вышеприведённого цикла:

        for (column in num_columns) {
     for (row in num_rows) {
         angle = (row / float(num_rows)) * PI
         grid[column][row] = angle
     }
}
    

Результат выглядит так:

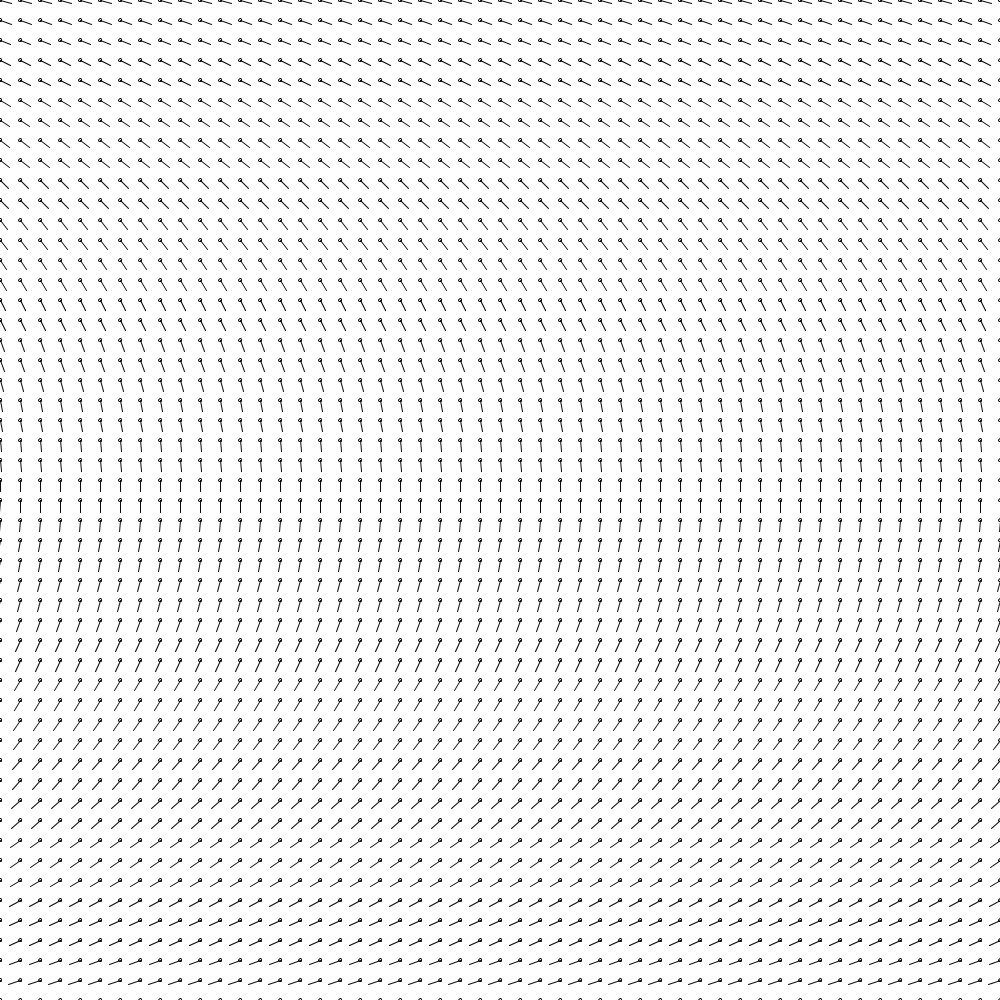
Рисуем линию в векторном поле

Теперь воспользуемся сеткой, чтобы нарисовать кривую:

1. Выбираем отправную точку.
2. Находим ближайший узел сетки, забираем указанный в нём угол.
   
3. Делаем небольшой шаг в соответствующем направлении, рисуя его на изображении.
   

Циклически повторяя пункты 1–3, рисуем линию.

        // отправная точка
x = 500
y = 100

begin_curve()

for (n in [0..num_steps]) {

    draw_vertex(x, y)

    x_offset = x - left_x
    y_offset = y - top_y

    column_index = int(x_offset / resolution)
    row_index = int(y_offset / resolution)

    // Замечание: обычно в этом месте нужно проверить границы
    grid_angle = grid[column_index][row_index]
    
    x_step = step_length * cos(grid_angle)
    y_step = step_length * sin(grid_angle)

    x = x + x_step
    y = y + y_step
}

end_curve()
    

Если мы выполним указанные действия для одной кривой, получим что-то похожее на следующий рисунок:

Нам нужно выбрать значения для нескольких ключевых параметров того, как мы рисуем кривые: длина шага step_length, число шагов num_steps и координаты начального положения (x, y).

Проще всего с параметром step_length. Как правило, он должен быть довольно мал, чтобы зритель не замечал отдельных точек на кривой. Порядка 0,1– 0,5% от ширины изображения. Можно делать больше для быстрой отрисовки или меньше, если на изображении линия круто изгибается и повороты должны остаться гладкими.

Другие переменные нуждаются в более длительном обсуждении, представленном в двух следующих разделах.

Выбор числа шагов

Значение num_steps кривой влияет на текстуру результата. Короткие линии больше похожи на мех, длинные кривые – на гладкие длинные волосы. Ниже пара примеров запуска одной и той же программы с разными значениями num_steps.

Обратите внимание, что первый рисунок ощущается более грубым, пятнистым, шероховатым, но плоским, второй – гладкий, спокойный и объёмный. Глаз скользит по второму рисунку, выявляя закономерности задавшего его векторного поля.

Ещё одно соображение касается смешения цветов. Более короткие линии позволяют лучше разделять участки рисунка с различным цветом, тогда как линии подлиннее как бы переносят цвет из одной области в другую. При игре с богатой палитрой полезно использовать короткие и средние по длине линии, если нужно избежать растянутых областей цветовых переходов. Сравните:

С другой стороны, если в палитре используются похожие цвета, хорошо работает переход к более длинным кривым. Это позволяет зрителю лучше прочувствовать их отличие:

Выбор стартовых позиций

Все кривые должны где-то начинаться. Вот три полезных варианта выбора начальных точек:

1. Регулярная сетка.
   
2. Равномерный набор случайных точек.
3. Упаковка кругов.
   

Обычная сетка – самая простая и жёсткая по структуре, в ней не хватает дыхания. Равномерно распределённые случайные точки создают более рыхлый рисунок из сгустков и разреженных областей. Подход с круговой упаковкой имеет хороший баланс: особенности распределены равномерно, но с достаточным числом случайных вариаций. Если вы создаёте чёрно-белый рисунок из длинных линий, вы вряд ли заметите различия:

Но при использовании коротких линий разница очевидна:

Искажение векторного поля

Из описанного выше понятно, что искривление векторного поля задаёт форму кривых, влияет на петли, повороты и перекрытие линий. Для искажения можно использовать различные подходы. В качестве примеров рассмотрим два антипода: классический шум Перлина и негладкие искажения.

Шум Перлина

Шум Перлина даёт на двумерной плоскости гладкие непрерывные значения. Поэтому он часто используется для инициализации векторного поля. Этот тип генерации случайных чисел также имеет приятное разнообразие «масштаба» шума, особенности имеют разный размер.

Как это использовать в коде? Пусть функция noise() возвращает значения шума Перлина (от 0,0 до 1,0) с учётом некоторых координат. Вернёмся к коду инициализации. Вместо того, чтобы указывать default_angle, можно задавать углы в точках сетки с помощью noise():

        for (column in num_columns) {
  for (row in num_rows) {
      // Для работы с noise() может потребоваться учитывать шаг
      scaled_x = column * 0.005
      scaled_y = row * 0.005

      // используем значение с шумом Перлина в диапазоне от 0.0 до 1.0
      noise_val = noise(scaled_x, scaled_y)

      // транслируем значение шума в угол между 0 и 2pi
      angle = map(noise_val, 0.0, 1.0, 0.0, PI * 2.0)
      grid[column][row] = angle
  }
}
    

Шум Перлина это хороший инструмент для начала, но лучше попытаться придумать что-то своё. Хотя бы потому, что для подобных проектов такая инициализация используется слишком часто.

Негладкие искажения

Важный критерий выбора техники искажения – является ли она гладкой или нет. То есть происходитли переход между соседними векторами плавно, без резких скачков. Полезно поэкспериментировать с негладкими векторными искажениями. Простой пример – начать с шума Перлина, в котором угол каждого вектора округлён до определенного значения, например, кратного π/10.

Так мы получаем более скульптурные, каменистые формы. Если ограничиться лишь π/4, выйдет некоторое подобие грубой гравюры:

Или к примеру, для каждого ряда векторов можно выбрать случайный угол между 0 и π.

Сочетание методов

Каждый может придумать свою игру на векторном поле. Вот ещё несколько идей для вдохновения.

Задать дистанцию между кривыми. На каждом шаге построения кривой по сетке можно проверять, не находится ли рядом уже существующая кривая. Если это так – останавливаемся и начинаем строить новую кривую.

Вместо непрерывных кривых рисовать точки. В следующем примере к этому добавлены проверки, позволяющие избежать «столкновений» кривых.

Слегка искажать сетку углов на определенных итерациях рисования. Это разнообразит семейство получаемых кривых без их полного искажения.

Соединить соседние кривые и заполнить цветом промежуточное пространство. Так можно получить плавные, но не одинаковые по сечению, структуры.

Поместить в кадр объекты, которые исказят сетку вокруг себя. Внутри «жидкого» векторного потока появляются «твёрдые» объекты:

Заключение

Описанные подходы, конечно, не являются догмой. Это лишь общие концепции применения векторных полей для генерации изображений, а также некоторый идеи, которые позволяют получать сбалансированные рисунки. Больше примеров использования программирования для создания изображений вы найдёте на сайте автора оригинальной статьи.