🖼️ ТОП-5 структур данных для обработки изображений

В компьютерном зрении и обработке графики используются различные структуры данных, позволяющие эффективно представлять, анализировать и изменять изображения. Матрицы, графы, цепи, пирамиды и квадродеревья – все эти структуры играют важную роль в задачах сегментации, распознавания объектов и сжатия изображений. Давайте разберем их особенности, достоинства и недостатки.

Матрицы

Матрицы – одна из самых широко используемых структур данных в обработке изображений. Матрица представляет собой двумерный массив чисел, где каждый элемент соответствует определенному пикселю изображения. Эти числа обычно задают яркость пикселя (в градациях серого) или значение цветового канала (в RGB-изображениях). Вот пример матрицы для изображения в оттенках серого (чем больше число, тем ярче пиксель):

• Строки и столбцы соответствуют координатам пикселей.
• Значения представляют яркость (0 – черный, 255 – белый в 8-битной шкале).

В контексте обработки изображений у матриц есть несколько важных преимуществ:

• Простота доступа к данным. Можно легко обратиться к конкретному пикселю по его координатам: M[i][j], где i – строка, а j – столбец.
• Хранение пространственных отношений. Матрица сохраняет расположение пикселей относительно друг друга, а это сильно упрощает работу с соседними пикселями (например, при фильтрации изображений).
• Универсальность. Матрицы применяются для множества задач: от базовой обработки (изменение яркости, контрастности) до сложных алгоритмов (размытие, обнаружение границ, обработка текстур).

К недостаткам матриц относятся:

• Большой расход памяти. Хранение изображений в виде матриц требует значительного объема памяти, особенно для больших изображений. Например, цветное изображение Full HD (1920×1080) занимает 1920×1080×3 байта ≈ 6 мегабайт (3 – это число цветовых каналов в RGB).
• Ресурсоемкость. Операции над изображениями (например, повороты, аффинные преобразования) могут быть ресурсоемкими, поэтому в некоторых случаях используются более сложные структуры данных (пирамиды или квадродеревья).

Цепи

Цепи часто используются для описания границ объектов на изображении. Идея заключается в том, чтобы представить данные в виде последовательности, где соседние символы будут соответствовать соседним пикселям изображения. У цепей есть несколько преимуществ и недостатков.

Плюсы:

• Можно представить с помощью простых структур данных (списки, массивы).
• Подходят для решения ряда задач по распознаванию образов.

Минусы:

• Являются линейной структурой, не позволяющей напрямую описывать сложные пространственные отношения.
• Поиск информации о пикселях требует последовательного перебора всей структуры.

Цепные структуры данных чаще всего реализуют с помощью цепных кодов или RLE-кодирования. Цепные коды используют для представления границ объектов, а RLE – самих объектов.

Цепные коды

Наиболее популярным применением цепей является цепной код Фримена, который используется для представления границ объектов толщиной в один пиксель. Цепной код Фримена описывает границу, начиная с координаты определенного пикселя, и записывает последовательность символов, соответствующих движениям на один пиксель в заранее заданных направлениях.

В 8-направленной системе код Фримена задает движение следующим образом:

           7   0   1
    \  |  /
   6 - x - 2
    /  |  \
   5   4   3

    

То есть:

• 0 – вправо
• 1 – вверх-вправо
• 2 – вверх
• 3 – вверх-влево
• 4 – влево
• 5 – вниз-влево
• 6 – вниз
• 7 – вниз-вправо

Возьмем для примера это изображение:

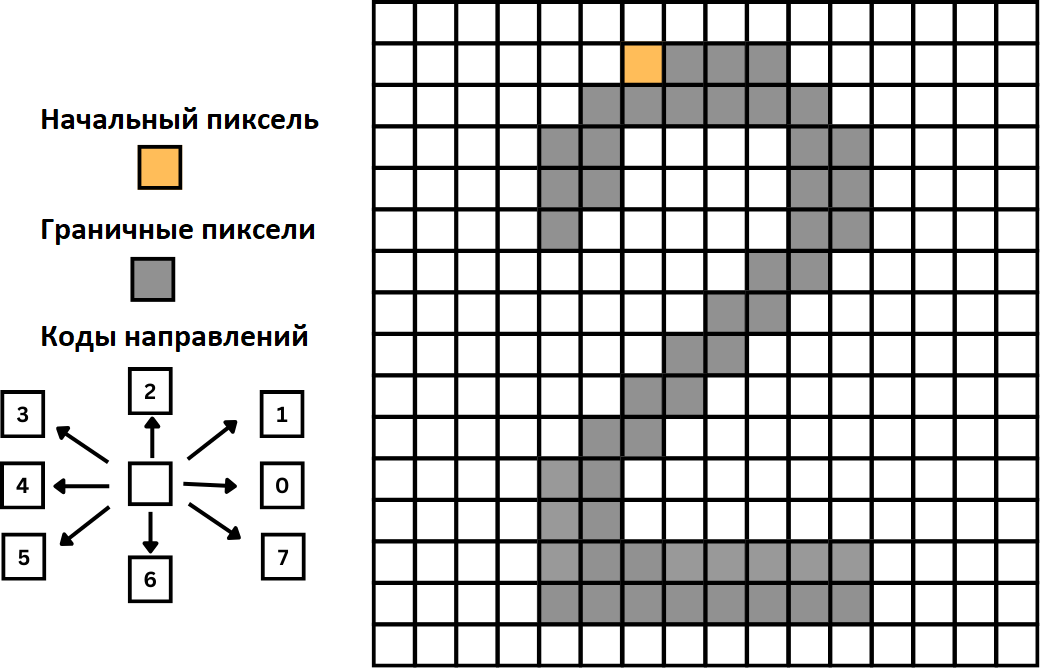
Если рассматривать оранжевый пиксель как начальную точку, соответствующий цепной код Фримена будет выглядеть так:

        00077665555556600000006444444442221111112234445652211

    

Эта последовательность указывает, в каком направлении следует двигаться, чтобы полностью обойти границу объекта.

Преимущества цепных кодов:

• Позволяют компактно хранить информацию о границах объектов.
• Отличаются простотой обработки и анализа.

Недостатки:

• Чувствительность к поворотам – одно и то же изображение при повороте может иметь совершенно другой код.
• Не предоставляют информацию о взаимном расположении объектов.

Прокачайте свои навыки алгоритмического мышления

Изучение алгоритмов и структур данных – это не просто академическое упражнение, а практический инструмент, который расширяет возможности каждого разработчика. Курс от Proglib Academy предлагает системный подход к этой фундаментальной области программирования.

Чему вы научитесь

• Освоите ключевые алгоритмы от базовых до продвинутых
• Разберетесь в сложности алгоритмов и О-нотации
• Изучите структуры данных: массивы, списки, деревья, хеш-таблицы
• Научитесь применять алгоритмические подходы: жадные алгоритмы, динамическое программирование
• Получите практический опыт решения задач, встречающихся на технических собеседованиях

Формат обучения

• 47 видеолекций от практикующих специалистов из Яндекса и ВШЭ
• 150 практических заданий с обратной связью от преподавателей
• Возможность учиться в своем темпе (от 3 часов в неделю)

Кодирование длин серий

Альтернативный способ использования цепей – кодирование длин серий (RLE), применяемое для представления объектов в изображении. В этом методе вместо хранения контура записываются только области, принадлежащие объекту.

Как работает RLE:

• Изображение представляется в виде матрицы пикселей.
• Записываются только те области, которые принадлежат объекту.
• Каждая строка изображения представляется списком, в котором первым элементом будет номер строки, а остальными элементами – пары координат (начало и конец последовательности пикселей объекта).

Допустим, у нас есть такое изображение:

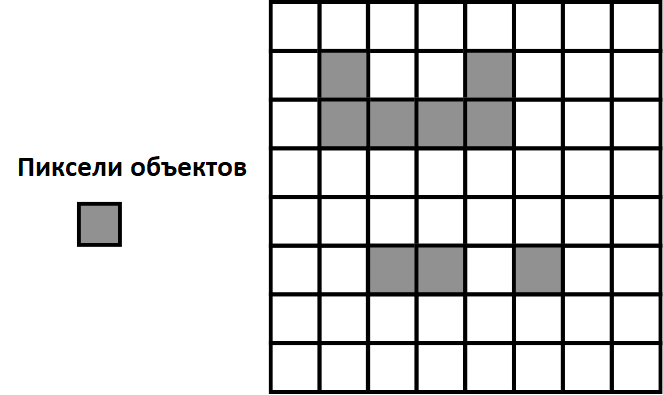
RLE-код для этих объектов будет выглядеть так:

        [[11144], [214], [52355]]

    

Преимущества RLC:

• Значительно снижает объем хранимых данных, если изображение содержит длинные однородные участки.
• Простота реализации.

Недостаток RLC – неэффективно для обработки изображений с высокой детализацией и множеством мелких объектов.

Графы

Графы – мощный инструмент для представления сложных пространственных структур и анализа связей между различными частями изображения.

В контексте обработки изображений узлы (вершины) графа обычно соответствуют разделенным регионам (областям, полученным после сегментации изображения), а дуги (ребра) показывают отношения между регионами (например, соседство).

Один из самых распространeнных типов графов в обработке изображений – граф смежности регионов (Region Adjacency Graph, RAG).

Как работает RAG:

• Каждая вершина графа представляет отдельную область в сегментированном изображении.
• Дуга проводится между двумя узлами, если их области граничат друг с другом.
• Граф явно хранит информацию о соседстве областей.

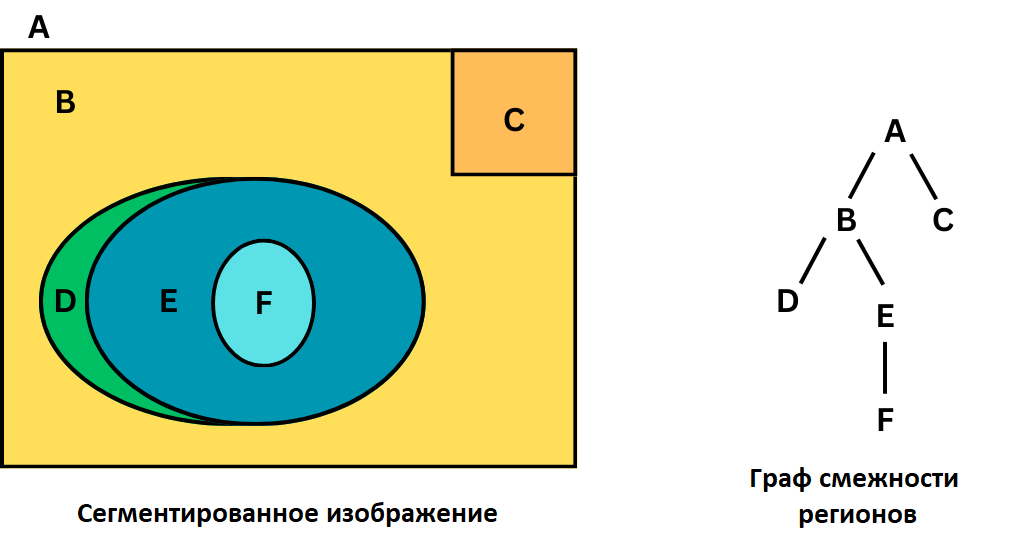
Использование графов дает ряд преимуществ:

• Эффективное представление пространственных отношений позволяет быстро находить соседние области, поэтому RAG очень широко используются в сегментации, распознавании объектов и анализе структур.
• Графовые разрезы позволяют находить замкнутые области – это необходимо при сегментации изображений и выделении объектов.
• Узлы со степенью 1 обозначают «простые дыры». Например, если у узла только одно соединение, это может означать, что внутри объекта есть замкнутая полость.
• В дугах можно хранить дополнительную информацию. К примеру, можно добавить атрибуты: "левее", "внутри", "рядом с" для улучшения анализа изображения.

Чтобы создать граф смежности регионов, нужно:

• Создать матрицу изображения, где каждому пикселю присвоен идентификатор области (например, после сегментации).
• Определить границы областей, проходя по матрице.
• Зафиксировать, какие регионы соседствуют друг с другом, создавая связи в графе.
• Сформировать граф, где каждая вершина – это область, а ребра соединяют соседние области.

Пирамиды

Пирамиды – иерархические структуры данных, которые представляют изображение на нескольких уровнях разрешения. Они полезны для алгоритмов, которым нужно работать с разными уровнями детализации одновременно.

Пирамидальная структура включает в себя последовательность изображений, где каждое следующее изображение создается на основе предыдущего, но с уменьшенным разрешением. Выглядит это так:

• Основание пирамиды (нижний уровень) – это исходное изображение в максимальном разрешении.
• Чем выше уровень пирамиды, тем меньше деталей в изображении.
• Вершина пирамиды (самый верхний уровень) может содержать буквально один пиксель, усредняющий всю информацию об изображении.

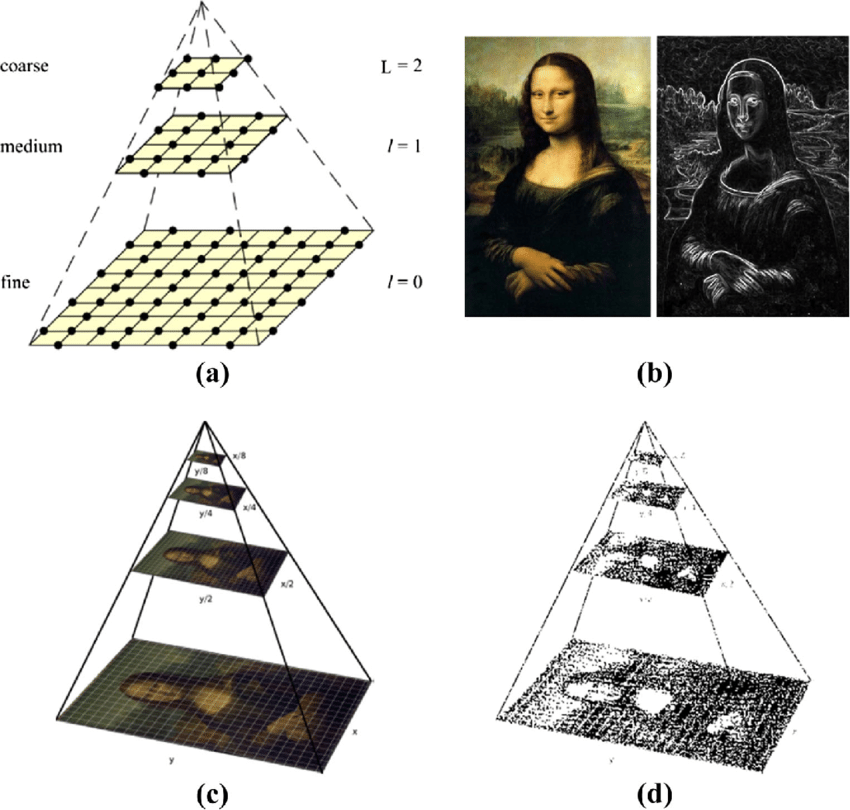
Зачем нужны пирамидальные структуры:

• Позволяют ускорить обработку изображения, так как на высоких уровнях пирамиды меньше пикселей.
• Помогают анализировать объекты разного размера без изменения масштаба фильтра.
• Используются в компьютерном зрении, например, для обнаружения объектов на разных уровнях детализации.

Существует два основных типа пирамид – матричные и древовидные.

М-пирамида

Матричная (M-пирамида) представляет собой последовательность изображений, где каждое следующее создается из предыдущего путем уменьшения разрешения в 2 раза. При этом:

• На нижнем уровне (основании) находится оригинальное изображение.
• На верхнем уровне остается один пиксель, содержащий обобщенную информацию обо всем изображении.

Пример использования M-пирамиды

Допустим, у нас есть алгоритм обнаружения птиц на изображении. Мы используем фиксированный шаблон для поиска птиц:

На разных уровнях пирамиды один и тот же шаблон может находить птиц разного размера (крупных в нижних уровнях, мелких — в верхних). Это избавляет от необходимости масштабировать шаблон и ускоряет процесс поиска.

Д-пирамида

В Д-пирамиде данные организуются в виде дерева, а не просто в последовательность уменьшенных изображений. При этом:

• Каждый узел дерева соответствует пикселю на определенном уровне разрешения.
• Листовые узлы (листья дерева) — это пиксели исходного изображения.
• Верхние уровни строятся на основе нижних, обычно путем усреднения значений дочерних узлов.

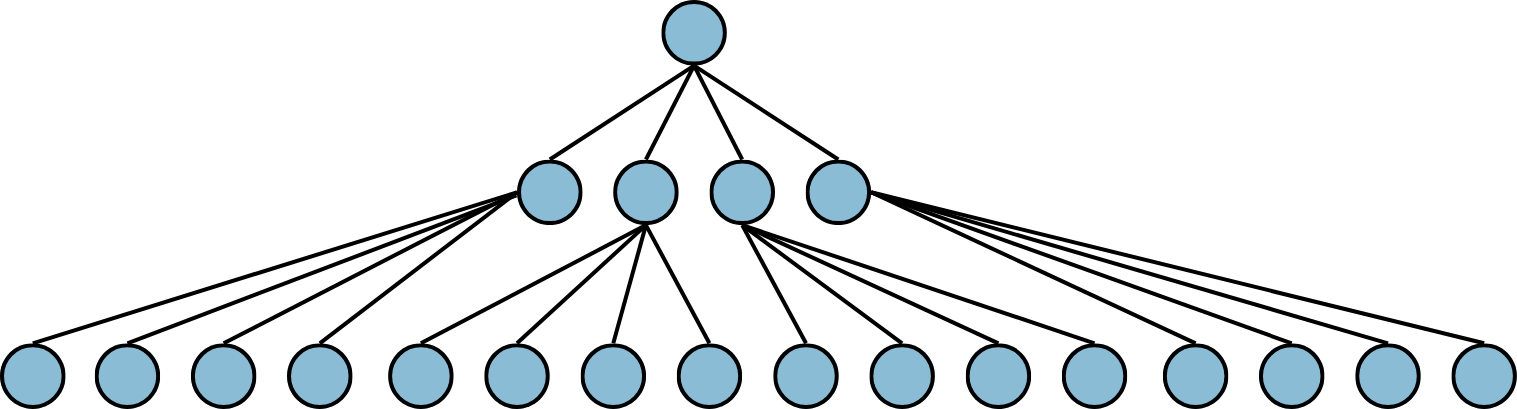
Пример использования Д-пирамиды

Если алгоритм обнаруживает резкие изменения контраста, то он может работать на низком разрешении, чтобы быстрее находить крупные границы. А если найдены мелкие детали, алгоритм может, напротив, переключаться на высокое разрешение, чтобы изучить их более точно.

Квадродеревья

Квадродерево — иерархическая структура данных, которая эффективно представляет изображения с большими однородными областями. Эта структура похожа на Д-пирамиду, но в ней каждый узел (кроме листовых) имеет ровно 4 дочерних узла.

Где используются квадродеревья:

• Сжатие изображений (JPEG 2000, фрактальное сжатие).
• Сегментация изображений (разделение на объекты и фон).
• Представление карт и рельефа (например, Google Maps использует квадродеревья для детализации).
• Рендеринг 3D-графики (оптимизация сцен).
• Поиск и распознавание объектов на фото.

Как работает квадродерево:

• Разделяем изображение на 4 равные части (квадранты).
• Проверяем каждый квадрант — eсли все пиксели внутри квадранта одинаковые, представляем его одним узлом в дереве. Если же пиксели разные, продолжаем делить квадрант на 4 подзоны.
• Повторяем процесс рекурсивно, пока в квадранте не останется только 1 пиксель, или весь квадрант не станет однородным (будет иметь одинаковый цвет/значение).

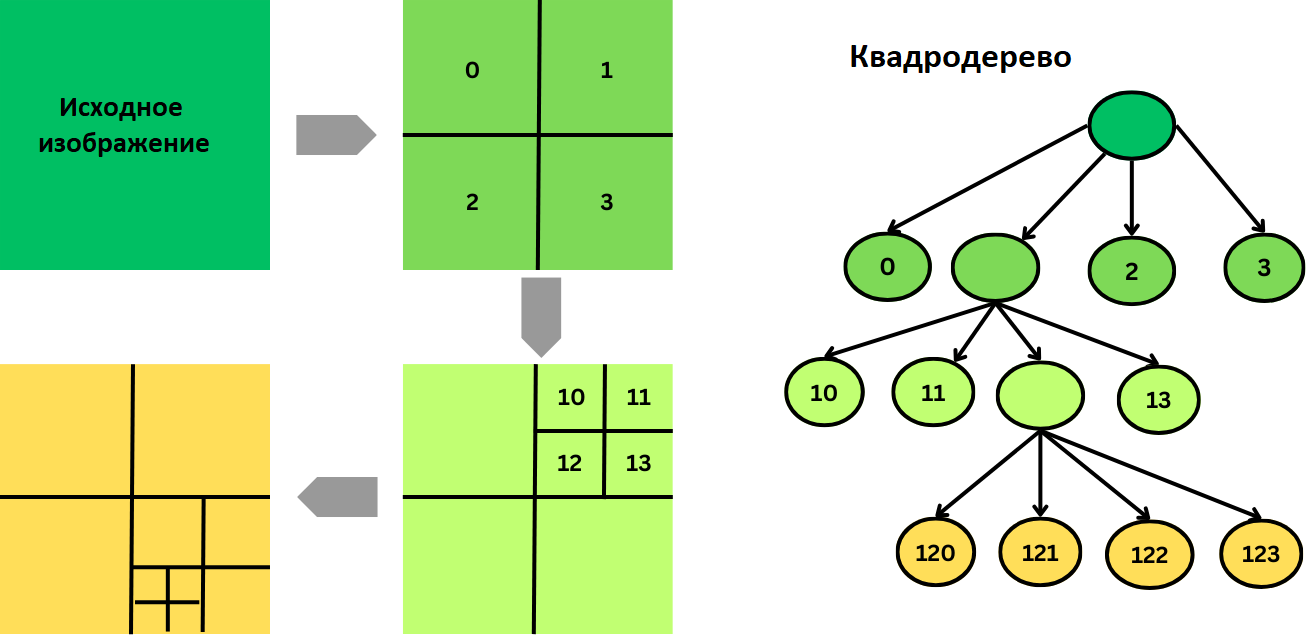
Преимущества квадродеревьев:

• Компактное представление данных. Вместо хранения каждого пикселя храним древовидную структуру, что экономит память, особенно если изображение содержит большие однородные зоны.
• Быстрые вычисления. Легко вычислять размер объектов, поскольку каждое деление содержит информацию об их площади.
• Эффективное объединение изображений. Два изображения можно легко сложить, используя структуру квадродерева.

Недостатки:

• Зависимость от положения, масштаба и относительного размера объектов. Даже незначительные манипуляции с изображением приводят к кардинальному изменению его квадродерева.
• Чувствительность к небольшим различиям. Два очень похожих изображения с небольшими различиями будут иметь совершенно разные квадродеревья.

Подведем итоги

Использование оптимальных структур данных в обработке изображений многократно повышает эффективность алгоритмов. Выбор конкретной структуры зависит от специфики задачи:

• Матрицы подходят для базовой обработки изображений, потому что обеспечивают простой и интуитивно понятный способ хранения и манипуляции пиксельными данными.
• Цепи используют для описания контуров, когда необходимо представить границы объектов в виде последовательности связанных точек. Это особенно важно в задачах распознавания форм и выделения объектов.
• Графы находят широкое применение в пространственном анализе и сегментации, поскольку позволяют устанавливать сложные топологические связи между элементами изображения.
• Пирамиды незаменимы для эффективной многоуровневой обработки и сжатия изображений, потому что хранят множество вариантов одного и того же изображения в различных разрешениях.
• Квадродеревья представляют собой особенно мощный инструмент для эффективного представления однородных областей в алгоритмах сжатия, рендеринга и поиска. Они позволяют значительно оптимизировать вычислительные процессы, разбивая изображение на иерархические секции и фокусируясь на наиболее значимых участках.

Грамотное применение этих структур позволяет ускорить вычисления и добиться более точных и качественных результатов, что делает их незаменимыми в компьютерном зрении, обработке медицинских снимков, геоинформационных системах и других областях, связанных с анализом изображений.