Деревья. Теория
Деревья расширяют идею связного списка. Кроме того, они позволяют узлам иметь более одного последующего узла, который связан с предыдущим.
Узлы дерева могут иметь любое количество дочерних узлов. Благодаря этому, данные представлены в виде гибкой схемы ветвления, что позволяет хранить и извлекать их с полной отдачей.
Один из типов деревьев – двоичное дерево поиска (BST – binary search tree). В предыдущих частях материала мы упоминали, насколько эффективно BST извлекают данные. Эта эффективность обусловлена двумя важными правилами, которые определяют структуру BST:
- Узел может иметь не более двух дочерних узлов.
- Каждый узел в левом поддереве должен содержать меньшее значение, а каждый узел в правом поддереве – большее.
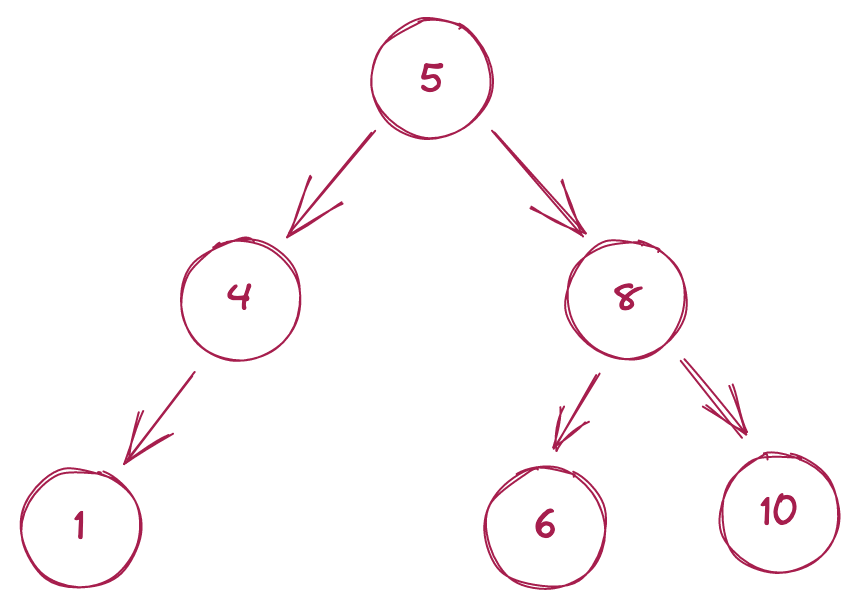
Поиск значения в BST занимает O(log n) времени. Это означает, что можно очень быстро найти требуемое значение среди миллионов или даже миллиардов записей.
Предположим, мы ищем узел со значением x. Чтобы быстро найти его в BST, воспользуемся следующим алгоритмом:
- Начать с корня дерева.
- Если x = значению узла: остановиться.
- Если x < значения узла: перейти к левому дочернему узлу.
- Если x > значения узла: перейти к правому дочернему узлу.
- Перейти к шагу 2.
При отсутствии уверенности в существовании искомого узла, необходимо изменить шаги 3 и 4 для остановки поиска.
Если хочешь подтянуть свои знания по алгоритмам, загляни на наш курс «Алгоритмы и структуры данных», на котором ты:
- углубишься в теорию структур данных;
- научишься решать сложные алгоритмические задачи;
- научишься применять алгоритмы и структуры данных при разработке программ.
Реализация
Создание узла TreeNode идентично созданию узла ListNode. Единственное отличие в том, что вместо одного атрибута у нас два: left и right, которые ссылаются на левые и правые дочерние узлы.
class TreeNode:
def __init__(self, val=None, left=None, right=None):
self.val = val
self.left = left
self.right = right
def __repr__(self):
return f"TreeNode со значением {self.val}"
Таким образом, мы создаем дерево с тремя уровнями. Стоит отметить, что данное дерево – просто бинарное, а не BST, потому что значения не отсортированы.
# Уровень 0
root = TreeNode('a')
# Уровень 1
root.left = TreeNode('b')
root.right = TreeNode('c')
# Уровень 2
root.left.left = TreeNode('d')
root.left.right = TreeNode('e')
root.right.left = TreeNode('f')
root.right.right = TreeNode('g')
# a
# / \
# b c
# / \ / \
# d e f g
Примеры
При работе с двоичными деревьями у нас могут возникнуть вопросы. Как правило, они касаются различных способов обхода узлов.
Обход дерева начинается с корневого узла. Далее, используем набор шагов для обработки каждого узла, включая дочерние. Порядок обработки узлов зависит от того, в какой последовательности идет подготовка родительского узла относительно дочерних: до (pre-order), между левым и правым (in-order) и после (post-order). На примерах, приведенных ниже, обход начинался с корневого узла. Однако, порядок обработки узлов был различен.
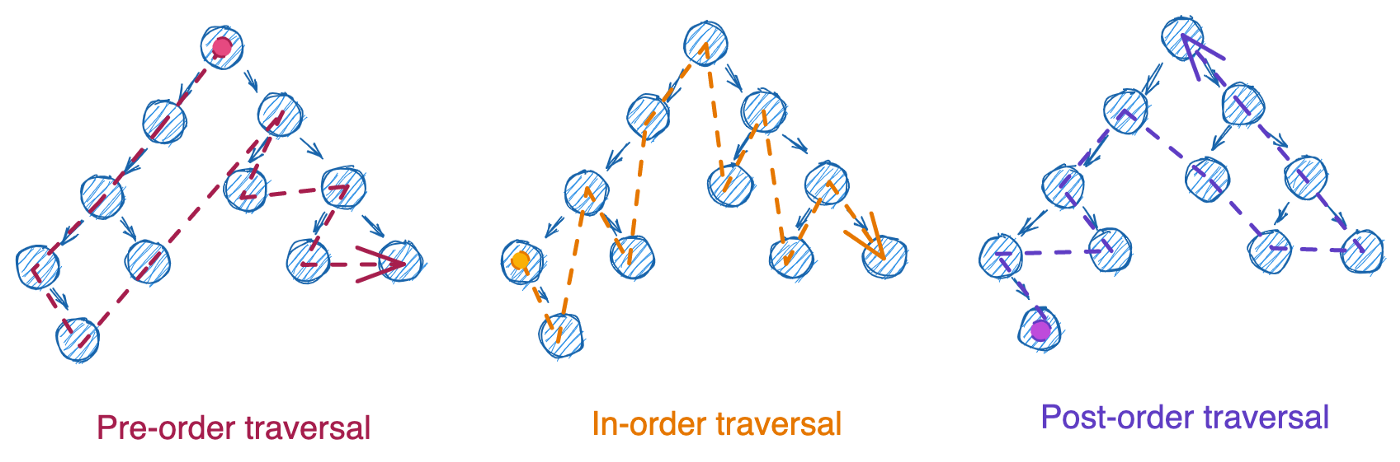
Эти три типа обхода могут быть реализованы следующими методами:
- с итерацией – использование цикла
whileи стека. В этом случае удаление данных возможно только с конца. - с рекурсией – использование функции, которая вызывает сама себя.
Есть четвертый тип обхода – порядок уровней (level-order traversal). Этот способ использует очередь (queue). Удаление данных здесь возможно только с начала.
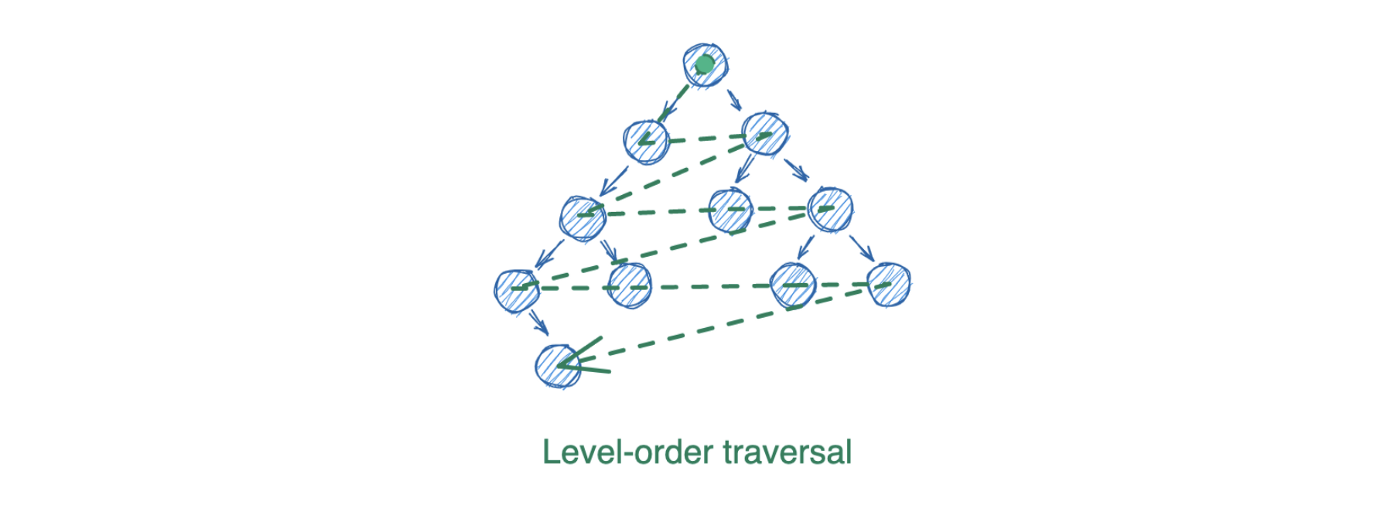
Для первых трех типов обработки узлов паттерны практически идентичны. Просто выберем обход в порядке возрастания. Ниже разберем итеративный и рекурсивный методы для LC 94: Binary Tree Inorder Traversal, начиная с итеративной версии:
# Итеративный обход
def traverse_in_order(root: TreeNode) -> List[int]:
"""
Обход двоичного дерева, возвращается список значений по порядку
"""
answer = []
stack = [(root, False)] # (узел, посещен ли он еще)
while stack:
node, visited = stack.pop()
if node:
if visited:
answer.append(node.val)
else:
stack.append((node.right, False))
stack.append((node, True))
stack.append((node.left, False))
return answer
Алгоритм действий:
- Строки 6-7: Создаем список для ответа (
answer) и для стека (stack).Listсодержит кортеж корневого узла и переменную False, которая указывает на то, что этот узел еще не был затронут. - Строка 9: Запускаем цикл
while. Он будет выполняться до тех пор, пока в стеке есть хотя бы один элемент. - Строки 10-12: Удаляем последний элемент из стека с помощью
.pop. Далее проверяем существованиеnode(узла). Node не всегда будет существовать в последующих итерациях для узлов без дочерних элементов. - Строки 14-15: Добавляем значение узла к ответу. Действие происходит только в том случае, когда node существует и мы уже затрагивали этот узел.
- Строки 16-19: Добавляем правый дочерний, текущий и левый дочерний узлы. На правый и левый узлы ставим пометку (флаг), которая показывает, что они не были проиндексированы на данном этапе выполнения программы. На текущий узел ставим флаг, который показывает, что он был замечен программой. Действие происходит до момента, когда мы посетили этот узел.
- Строки 9-19: Повторяем шаги 3-6, пока не обработаем все узлы.
- Строка 21: Возвращаем список значений узлов, которые отсортированы по порядку.
Примечание: Добавление узлов в стек (строки 17-19), может показаться неупорядоченным. Однако, стеки работают по принципу Last In First Out. Первый узел, который нужно обработать, должен быть последним узлом, который добавляется в стек. Поэтому, сначала добавляется правый, и только потом левый узел.
Далее расскажем о рекурсивном методе:
# Рекурсивный обход
class Solution:
def __init__(self):
self.answer = []
def traverse_inorder(self, root: TreeNode) -> List[Any]:
"""
Проходим двоичное дерево, и возвращаем список значений в порядке их следования
"""
self._traverse(root)
return self.answer
def _traverse(self, node: Optional[TreeNode]) -> None:
"""
Рекурсивная функция для последовательного обхода
"""
if not node:
return None
self._traverse(node.left)
self.answer.append(node.val)
self._traverse(node.right)
Алгоритм действий:
- Строки 2-4: Создаем класс, который инициализируется списком для ответа (
self.answer). - Строки 6-11: Определяем функцию
traverse_inorder, которая принимает корневой узел дерева, вызывает рекурсивную функцию _traverse и возвращает self.answer. - Строки 13-22: Определяем рекурсивную функцию
_traverse, которая принимает узел. Функция проверяет существованиеnodeперед тем как вызвать саму себя на левом дочернем узле. Далее она добавляет значение узла кself.answer. Затем повторно происходит операция самовызова уже на правом дочернем узле.
Подведем итоги. Данные примеры мы рассматривали в контексте обхода in-order. Для того чтобы изменить порядок следования на pre-order или post-order, в обоих случаях нужно поменять порядок обработки узла относительно его дочерних элементов. Остальная часть кода остается неизменной.
# Изменение обхода
def iterative(root):
...
stack.append((node.right, False))
stack.append((node.left, False))
stack.append((node, True)) # <- изменение
...
def _traverse(self, node):
...
self.answer.append(node.val) # <- изменение
self._traverse(node.left)
self._traverse(node.right)
Графы. Теория
Деревья расширяют область применения связанных списков, позволяя иметь более одного дочернего узла. При помощи графов можно расширить область применения и ослабить строгую «родительскую» связь в деревьях. Узлы графа не имеют явной иерархии. Каждый узел может быть соединен с любым другим узлом.
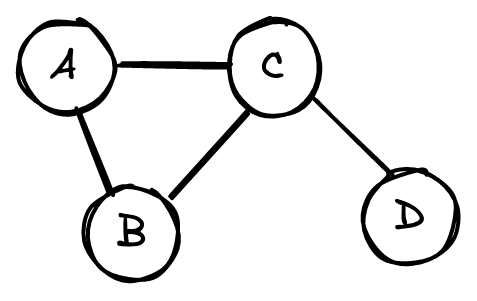
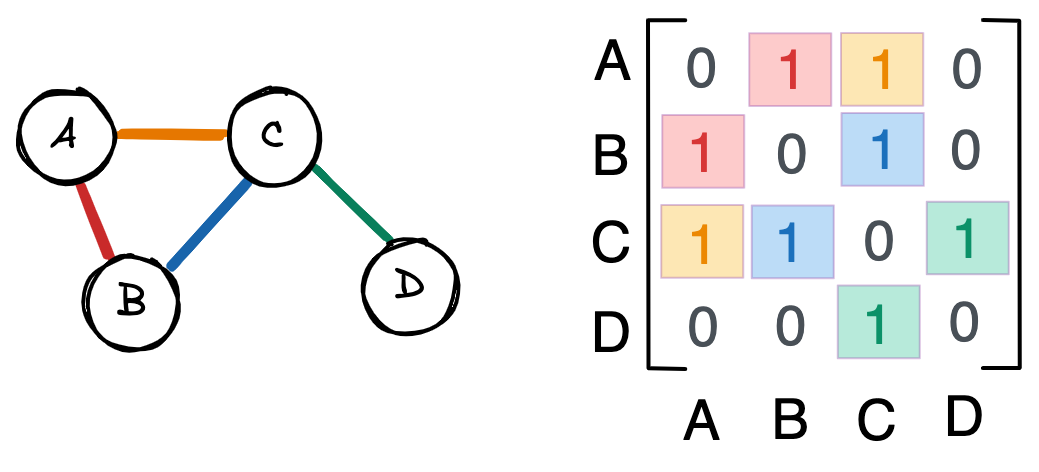
Как правило, графы представлены в виде матриц смежности (adjacency matrix). Так, у приведенного выше графа будет следующая матрица.

Каждая строка и столбец представляют собой узел. Единица в строке i и столбце j, или A_{ij}=1, означает связь между узлом i и узлом j.
A_{ij}=0 означает, что узлы i и j не связаны.
Ни один из узлов в этом графе не связан с самим собой. Следовательно, диагональ матрицы равна нулю. Аналогично, A_{ij} = A_{ji}, потому что связи ненаправленны. То есть если узел A связан с узлом B, то B связан с A. В результате матрица смежности симметрична по диагонали.
Рассмотрим пример, который поможет нам понять описанную выше теорию.
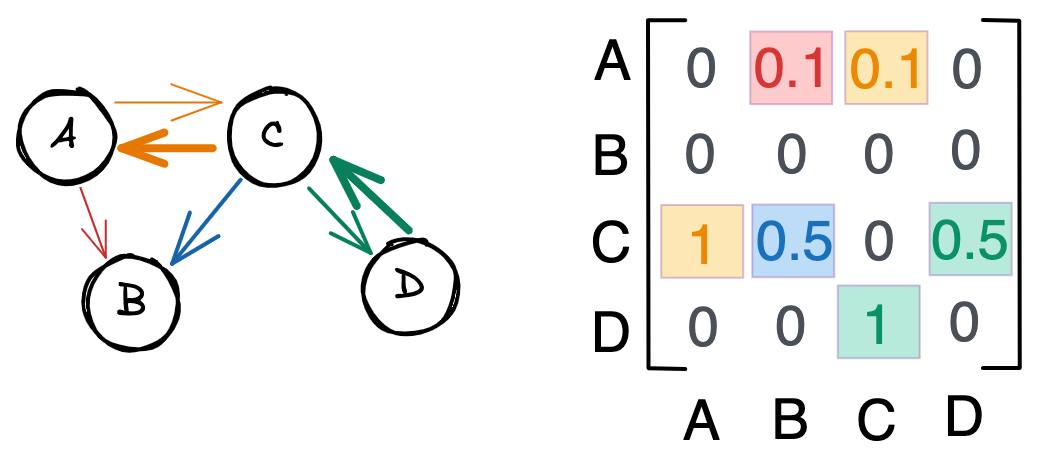
На представленных рисунках мы видим взвешенный граф с направленными ребрами. Обратите внимание, что связи больше не симметричны – вторая строка матрицы смежности пуста, потому что у B нет исходящих связей. Числа от 0 до 1 отражают силу связи. Например, граф C влияет на граф A сильнее, чем A на C.
Реализация
Реализуем невзвешенный и неориентированный граф. Основной структурой класса является список списков Python. Каждый из них – это строка. Индексы в списке представляют собой столбцы. При создании объекта Graph необходимо указать количество узлов n, чтобы создать список списков. Затем мы можем получить доступ к соединению между узлами a и b с помощью self.graph[a][b].
from typing import List
class Graph:
def __init__(self, n: int):
self.graph = [[0]*n for _ in range(n)]
def connect(self, a: int, b: int) -> List[List[int]]:
"""
Обновляем self.graph для соединения узлов A и B.
"""
self.graph[a][b] = 1
self.graph[b][a] = 1
return self.graph
def disconnect(self, a: int, b: int) -> List[List[int]]:
"""
Обновляем self.graph для разъединения узлов A и B.
"""
self.graph[a][b] = 0
self.graph[b][a] = 0
return self.graph
Воссоздать график из первого примера можно следующим образом:
g = Graph(4)
# соединения A
g.connect(0, 1)
g.connect(0, 2)
# соединения B (исключая A)
g.connect(1, 2)
# соединения C (исключая B)
g.connect(2, 3)
Пример
Одним из сложных вопросов в теории графов является определение количества связанных компонентов или подкластеров внутри графа. Например, в приведенном ниже графе можно выделить три различных компонента.
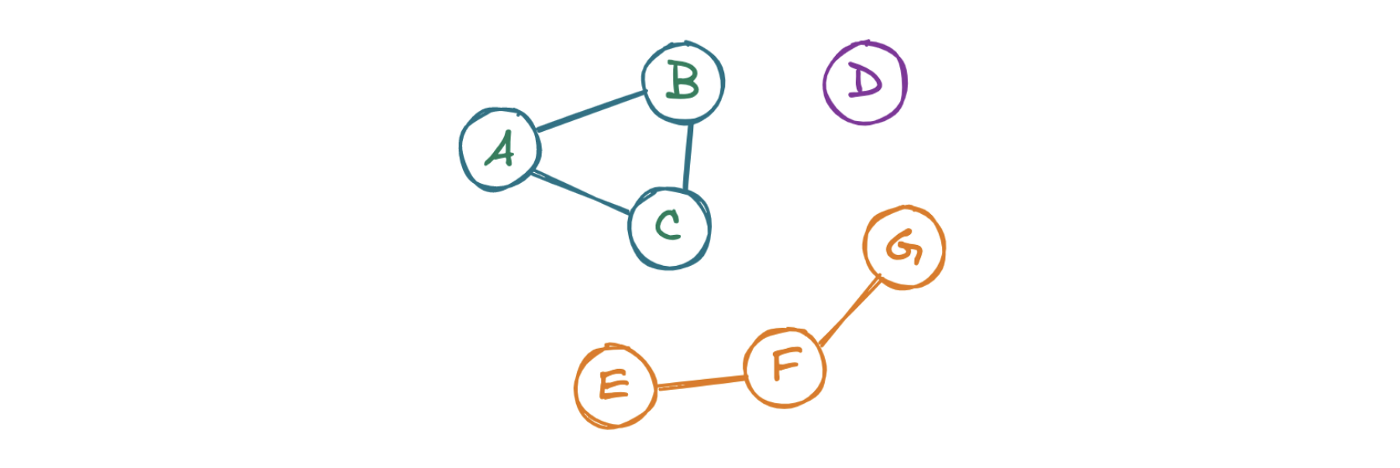
Чтобы ответить на вопрос LC 323: Количество связных компонентов, изучим каждый узел графа. Далее «посетим» соседние графы. Повторяем операцию до тех пор, пока не встретим только те узлы, которые уже были замечены программой. После этого проверим наличие в графе узлов, которые еще не были замечены. Если такие узлы присутствуют, то существует еще как минимум один кластер, поэтому нужно взять новый узел и повторить процесс.
def get_n_components(self, mat: List[List[int]]) -> int:
"""
Учитывая матрицу смежности, возвращает количество связанных компонентов
"""
q = []
unseen = [*range(len(mat))]
answer = 0
while q or unseen:
# Если все соседние узлы прошли через цикл, переходим к новому кластеру
if not q:
q.append(unseen.pop(0))
answer += 1
# Выбираем узел из текущего кластера
focal = q.pop(0)
i = 0
# Поиск связей во всех оставшихся узлах
while i < len(unseen):
node = unseen[i]
# Если узел подключен к центру, добавляем его в очередь
# чтобы перебрать его соседей
# из невидимых узлов и избежать бесконечного цикла
if mat[focal][node] == 1:
q.append(node)
unseen.remove(node)
else:
i += 1
return answer
Алгоритм действий:
- Строки 5-8: Создаем очередь (
q), список узлов (unseen) и количество компонентов (answer). - Строка 10: Запускаем цикл
while, который выполняем до тех пор, пока в очереди есть узлы, которые нужно обработать или узлы, которые не были замечены. - Строки 13-15: Если очередь пуста, удаляем первый узел из непросмотренных и увеличиваем количество компонентов.
- Строки 18-19: Выбираем следующий доступный узел в очереди (
focal). - Строка 22: Запускаем цикл
while, который выполняем до тех пор, пока не обработаем все оставшиеся узлы. - Строка 23: Даем имя текущему узлу для оптимизации кода.
- Строки 28-30: Если текущий узел подключен к центру, добавляем его в очередь узлов текущего кластера. Удаляем его из списка тех узлов, которые могут находиться в невидимом кластере. Благодаря этому действию, мы избегаем бесконечного цикла.
- Строки 31-32: Если текущий узел не подключен к
focal(центру), переходим к следующему узлу.
Заключение
Графы и деревья – основные структуры данных. Спектр их применения огромен. Например, графы используются там, где необходим алгоритм поиска решений. Реальный пример их использования – sea-of-nodes JIT-компилятора.
Деревья используются тогда, когда мы должны произвести быстрое добавление/удаление объекта с поиском по ключу. Например, в различных словарях и индексах БД (Баз данных). Кроме того, деревья являются неотъемлемой частью случайного леса – алгоритма машинного обучения.
В следующей части материала мы приступим к изучению хэш-таблиц.
Базовый и продвинутый курс «Алгоритмы и структуры данных» включает в себя:
- Живые вебинары 2 раза в неделю.
- 47 видеолекций и 150 практических заданий.
- Консультации с преподавателями курса.


Комментарии